Consider the parabola x2+4y=0. Let P(a,b) be any fixed point inside the parabola and let S be the focus of the parabola. Then the minimum value at SQ+PQ as point Q moves on the parabola is
|1−a|
|ab|+1
√a2+b2
1−b
The correct Answer is:D
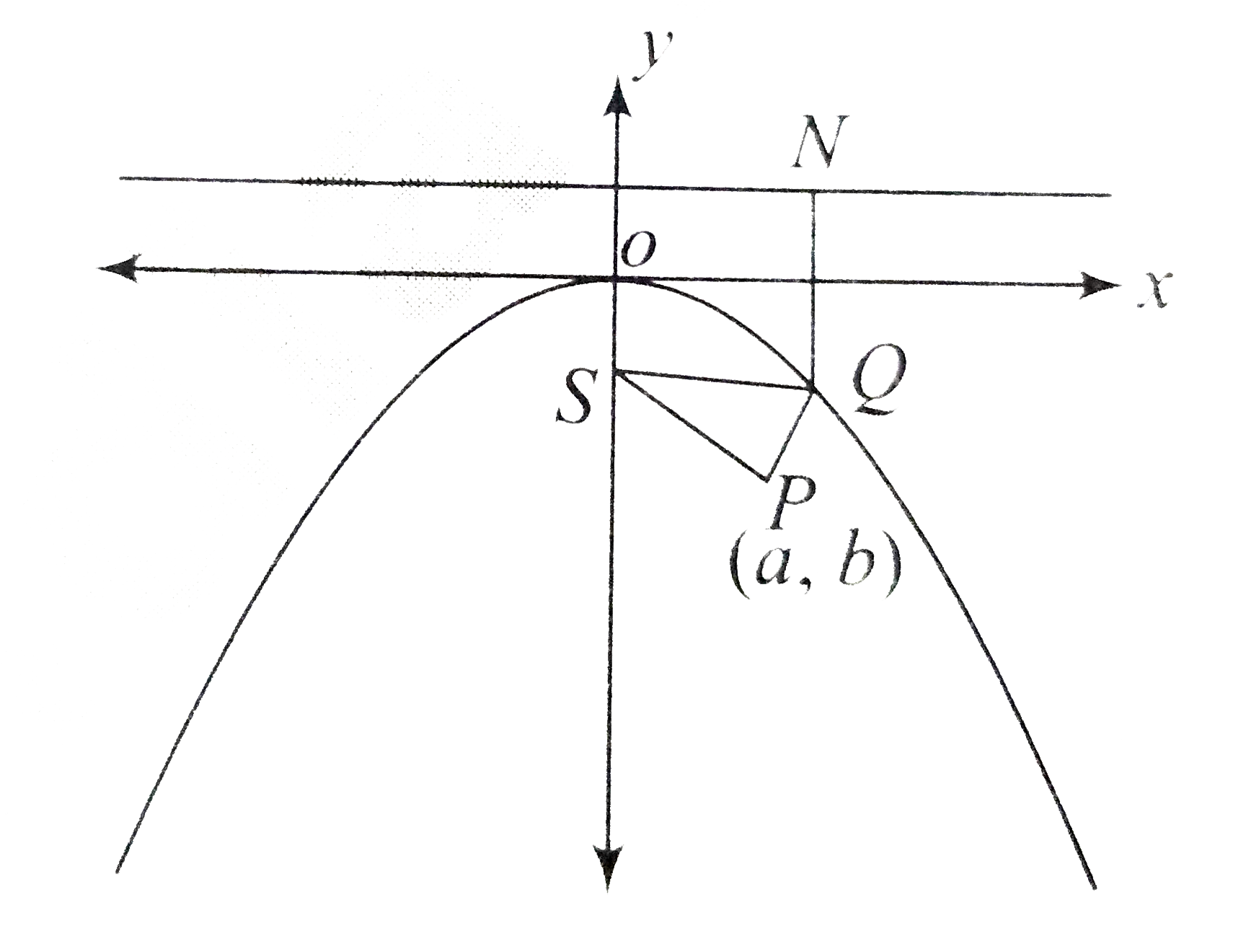
Let the foot of perpendicular from Q to the directrix be N.
SQ+PQ=QN+PQ is minimum when P, Q and N are collinear. So, minimum value of SQ+PQ=PN=1−b
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Advenced Single Answer Type
18 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
19 Videos
Similar Questions
Consider the parabola x2=4y and the point F(0,1). let
View SolutionConsider the parabola y2=4x .A=(4,-4) and B=(9,6) "be two fixed point on the parabola"." Let 'C' be a moving point on the parabola between "A" and "B" such that the area of the triangle ABC is maximum then the co-ordinate of 'C' is
View Solution
Knowledge Check
Consider the parabola y2=4x, let P and Q be two points (4,−4) and (9,6) on the parabola. Let R be a moving point on the arc of the parabola whose x-coordinate is between P and Q. If the maximum area of triangle PQR is K, then (4K)1/3 is equal to
A1B2C5D7Let P(4,−4) and Q(9,6) be points on the parabola y2=4a(x−b). Let R be a point on the arc of the parabola between P and Q. Then the area of ΔPQR is largest when.
A∠PRQ=π2Bthe point R is (4,4)Cthe point R is (14,1)DNone of theseConsider a parabola x2−4xy+4y2−32x+4y+16=0.
The focus of the parabola (P) isA(2,1)B(-2,1)C(-2,-1)D(2,-1)
Consider the parabola with vertex (12,34) and the directrix y=12. Let P be the point where the parabola meets the line x=−12. If the normal to the parabola at P intersects the parabola again at the point Q, then (PQ)2 is equal to :
View SolutionConsider the parabola with vertex (12,34) and the directrix y=12. Let P be the point where the parabola meets the line x=−12. If the normal to the parabola at P intersects the parabola again at the point Q, then (PQ)2 is equal to :
View SolutionConsider a parabola x2−4xy+4y2−32x+4y+16=0.
The focus of the parabola (P) is
View SolutionIf P is the point (1,0) and Q is any point on the parabola y2=8x then the locus of mid - point of PQ is
View SolutionThe normal at a point P to the parabola y2=4x is parallel to the tangent at Q√2,2 to the hyperbola nd meets the axis of the parabola at If 5 is the focus of the parabola, area of the triangle PSR in sq. units is
View Solution
