A normal to parabola, whose inclination is 30∘, cuts it again at an angle of
tan−1(√32)
tan−1(2√3)
tan−1(2√3)
tan−1(12√3)
The correct Answer is:D
The normal at P(at21,2at1) is y+xt1=2at1+at31 with slope say tanα=−t1=1√3.
If it meets curve at Q(at22,2at2) then t2=−t1−2t1=−7√3.
Then angle θ between parabola (tangent at Q) and normal at P is given by
tanθ=∣∣
∣
∣∣−t1−1t21−t1t2∣∣
∣
∣∣=12√3
⇒θ=tan−1(12√3)
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Advenced Single Answer Type
18 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
19 Videos
Similar Questions
Knowledge Check
A noraml to the parabola at a point A on the parabola whose equation is y2=2013x cuts the axis of x at N. AN is produced to the point B such that NB=12AN.
If the normals through any point of the parabola y^(2)=2013x, cut the line 2x - 2013 = 0, in points whose ordinates are in AP, then the slopes of these normals are inAAPBGPCHPDnone of theseA noraml to the parabola at a point A on the parabola whose equation is y2=2013x cuts the axis of x at N. AN is produced to the point B such that NB=12AN.
If two more normals to the parabola y2=2013x pass through B, then they areAcoincidentBinclined at π4Cinclined at π6Dinclined at π2Consider a parabola y2=4ax, if the normal to the parabola at the point (at2,2at) cuts the parabola again at(aT2,2aT), then
AT2≥8BT2≤6CT∈(−∞,−8)∪(8,∞)DNone of these
If the normal to the parabola y2=4ax at point t1 cuts the parabola again at point t2 , then prove that t22≥8.
View SolutionIf the normal to the parabola y2=4ax at point t1 cuts the parabola again at point t2.Then the minimum value of t22 is
View SolutionA block is kept on a rought incline whose angle of inclination is greater than angle of repose.
(a) Find the minimum and maximum force F applied parallel to incline that will keep it in equilibrium.
(b) What is the required force if it is applied normal to the incline?
(c) What is the range of F if it is applied horizontally on the block?
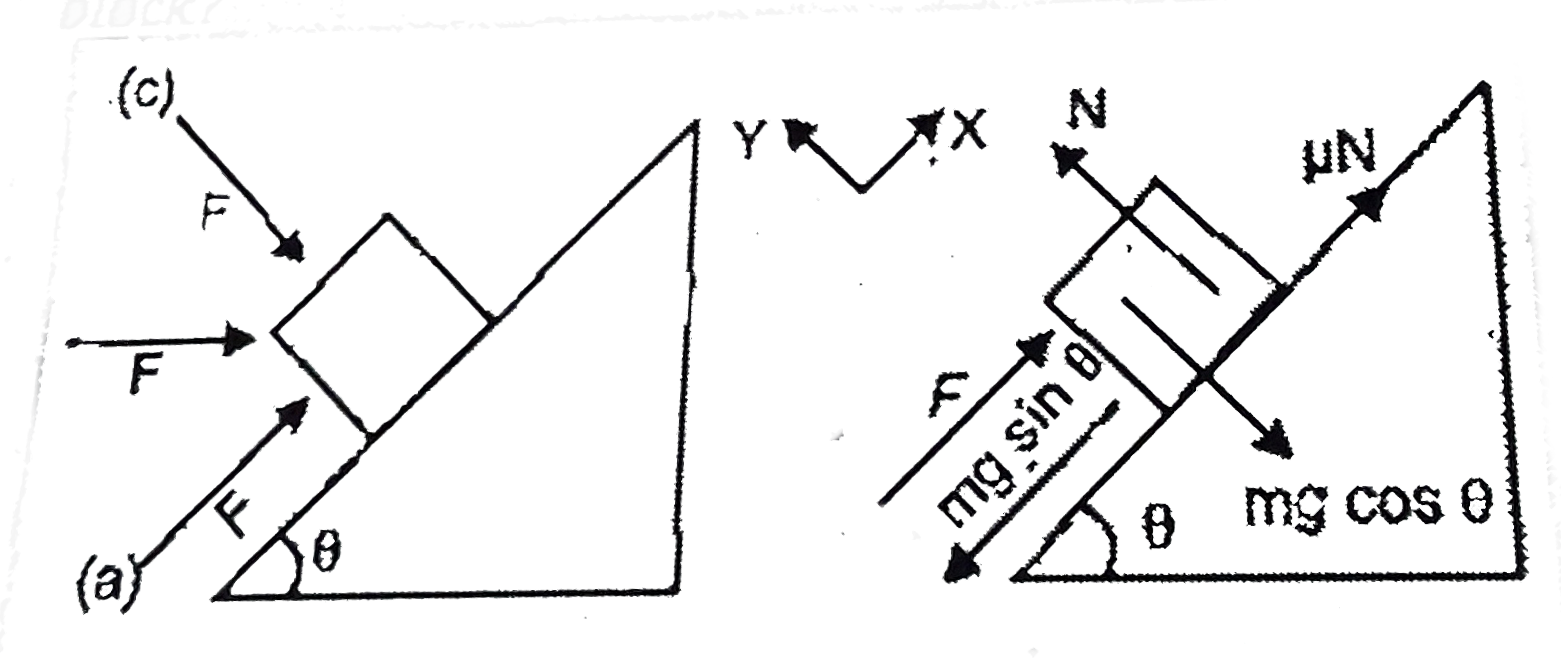
View SolutionA normal to the parabola at a point A on the parabola whose equation is y2=2013x cuts the axis of x at N. AN is produced to the point B such that NB=12AN.
If C is a point on the parabola y2=2013x such that OCN=π2 (O being origin), then projection of CN on x-axis is equal to
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View Solution
