If the normal at a point P to the hyperbola meets the transverse axis at G, and the value of SG/SP is 6, then the eccentricity of the hyperbola is (where S is focus of the hyperbola)
A
2
B
4
C
6
D
8
Text Solution
The correct Answer is:C
Equation of normal at point P(asecθ,btanθ) on hyperbola x2a2−y2b2=1 is
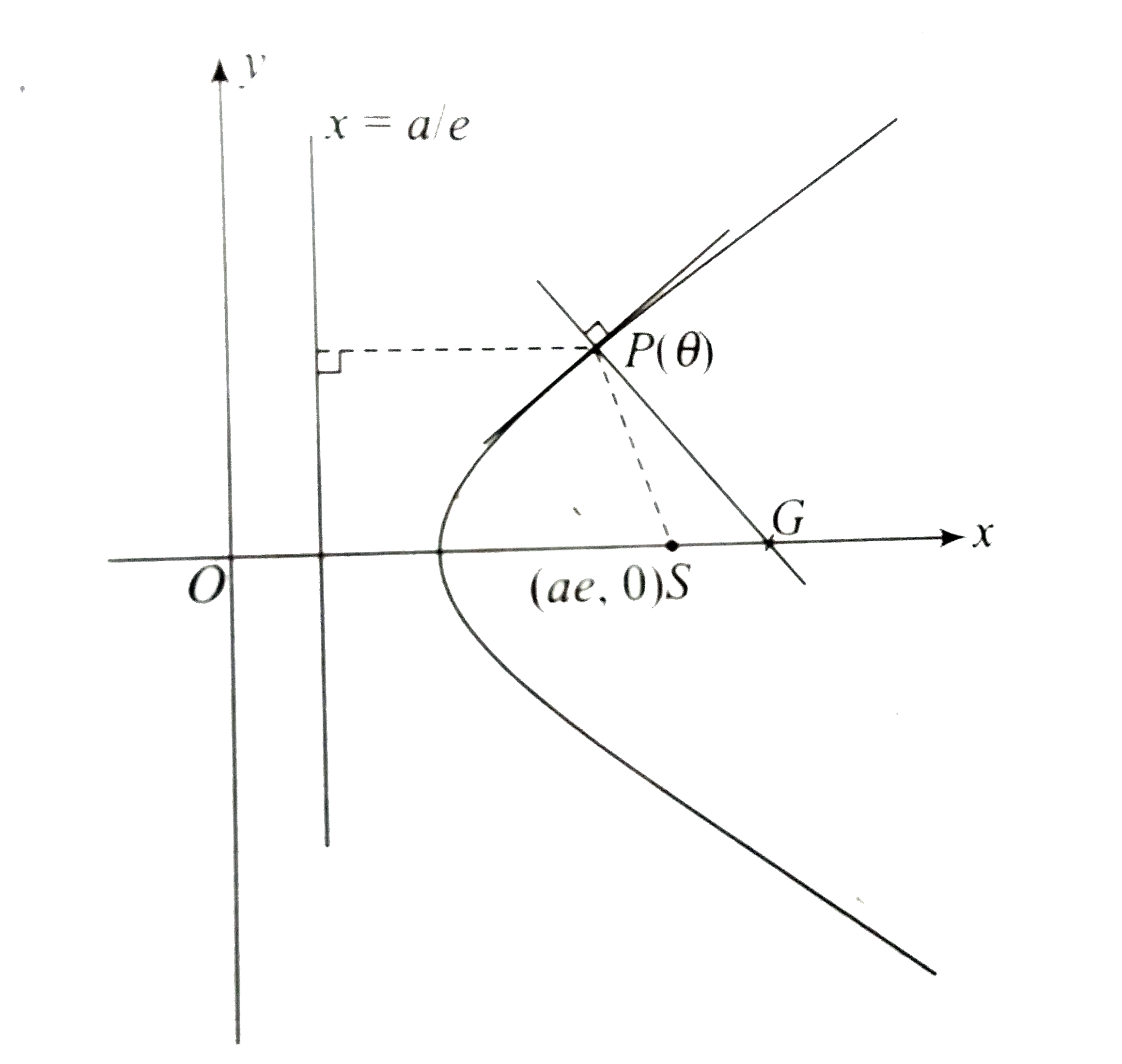
acosθx+bcotθy=a20+b2
∴G(a2+b2acosθ,0)
S(ae,0)
SP=e(asecθ)−a
Also SG=a2+b2acosθ−ae=a2e2acosθ−ae=e[e(asecθ)−a]
⇒SG/SP=e=6
|
Similar Questions
Knowledge Check
If the normal at P on the hyperbola meets the transverse axis at G, S is a foci and the eccentricity of the hyperbola then SG : SP is equal to
AaBbCeD1/eIf the normal at P to the rectangular hyperbola x2−y2=4 meets the axes at G and gandC is the center of the hyperbola, then PG=PC (b) Pg=PC PG−Pg (d) Gg=2PC
APG = PCBPg = PCCPG = PgDGg = 2PCIf the normal at the point P intersects the x-axis at (9, 0) then the eccentricity of the hyperbola is
A√52B√32C√2D√3
Find the eccentricity of the hyperbola whose latusrectum is half of its transverse axis.
View SolutionIf asymptotes of hyperbola bisect the angles between the transverse axis and conjugate axis of hyperbola, then what is eccentricity of hyperbola?
View SolutionIf the normal at 'θ' on the hyperbola x2a2−y2b2=1 meets the transverse axis at G, and A and A' are the vertices of the hyperbola , then AC.A'G=
View SolutionFind the eccentricity of the hyperbola whose latusrectum is half of its transverse axis.
View SolutionIf the latus rectum of a hyperbola subtend an angle of 60A∘ at the other focus, then eccentricity of the hyperbola is
View Solution
