A tangent is drawn at any point on the hyperbola x2a2−y2b2=1. If this tangent is intersected by the tangents at the vertices at points P and Q, then which of the following is/are true
S,S',P and Q are concyclic
PQ is diameter of the circle
S,S', P and Q forms rhombus
PQ is diagonal of acute angle of the rhombus formed by S,S',P and Q
The correct Answer is:A, B
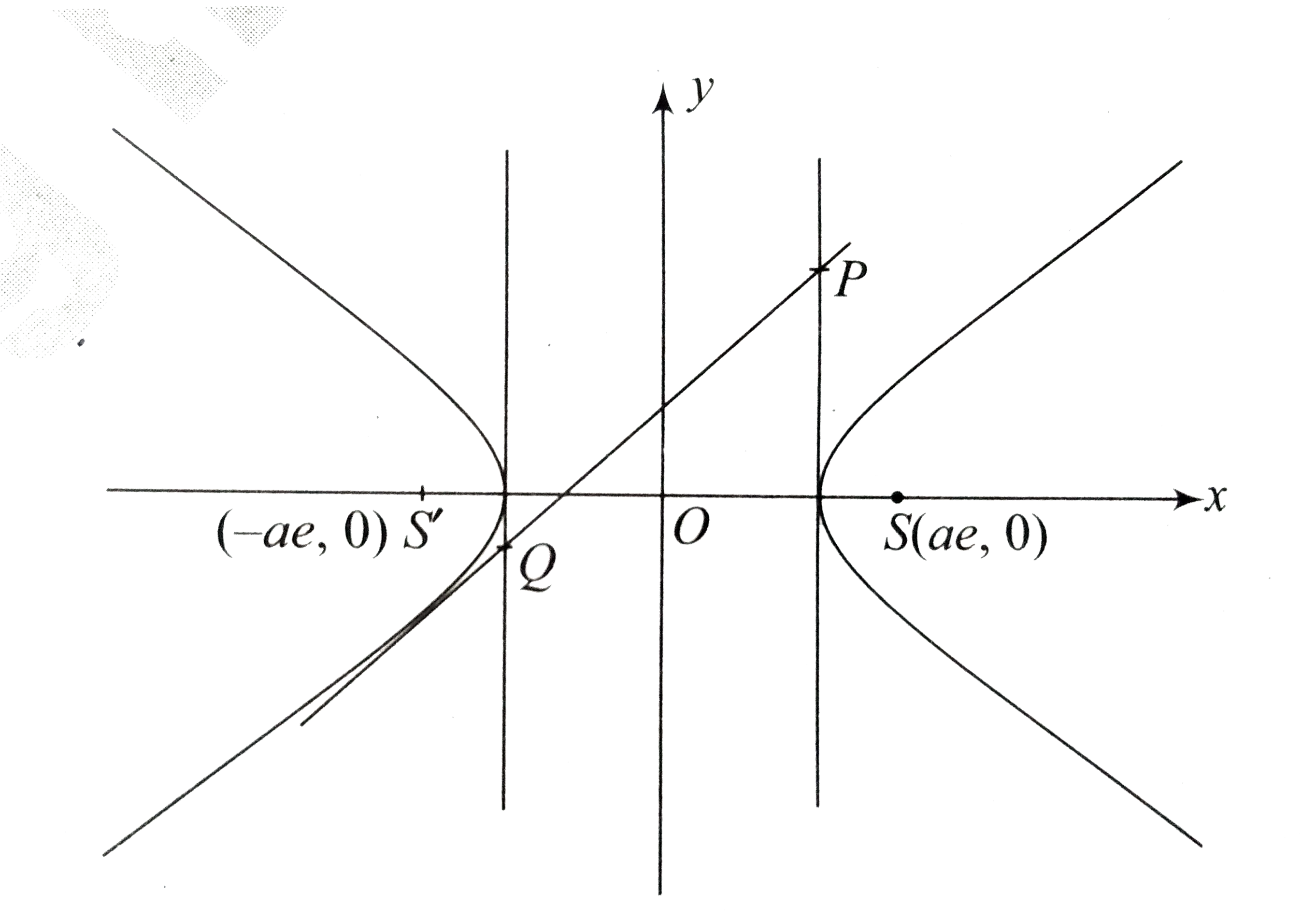
Any tangent to the hyperbola is xsecθa−ytanθb=1 Solving this line with the lines x=±a, we get the coordinates of points P and Q as
(a,btan.θ2) and (−a,−bcot.θ2)
Now slopes of the lines PS and QS are
mPS=btan.θ2a(1−e),mQS=−bcot.θ2−a(1+e)
⇒mPS.mQS=−b2a2(e2−1)=−1
Similarly mPS.mQS'=−1
⇒ line PQ subtends and angle of π2 at S and S'
⇒ points P,Q,S and S' are concyclic.
⇒PQ is diameter.
Similar Questions
A tangent is drawn at any point on the hyperbola x2a2−y2b2=1. If this tengent is intersected by the tangents at the vertices at points P and Q then show that S, S' , P and Q are concyclic points where S and S' are the foci of the hyperbola .
View SolutionTangents at any point P is drawn to hyperbola x2a2−y2b2=1 intersects asymptotes at Q and R, if O is the centre of hyperbola then
View Solution
Knowledge Check
From a point P, two tangents PA and PB are drawn to the hyperbola x2a2−y2b2=1. If these tangents cut the coordinates axes at 4 concyclic points, then the locus of P is
Ax2−y2=∣a2−b2∣∣Bx2−y2=a2+b2Cx2+y2=∣∣a2−b2∣∣Dx2+y2=a2+b2Tangents at any point P is drawn to hyperbola x2a2−y2b2=1 intersects asymptotes at Q and R, if O is the centre of hyperbola then
AArea of triangle OQR is abBArea of triangle OQR is 2abCP is mid-point of QRDP trisect QRFrom a point P, two tangents PA and PB are drawn to the hyperbola x2a2−y2b2=1. If the product of the slopes of these tangents is 1, then the locus of P is a conic whose eccentricity is equal to
A1B2C√2D12
Two tangents are drawn to the hyperbola x2a2−y2b2=1 such that product of their slope is c2 . the locus of the point of intersection is
View SolutionTangents are drawn from a point on the circle x2+y2=11 to the hyperbola x236−y225=1 ,then tangents are at angle:
View SolutionThe point of intersection of tangents drawn to the hyperbola x2a2−y2b2=1 at the points where it is intersected by the line lx+my+n=0 is
View SolutionFrom a point P, two tangents PA and PB are drawn to the hyperbola x2a2−y2b2=1. If the product of the slopes of these tangents is 1, then the locus of P is a conic whose eccentricity is equal to
View SolutionIf tangents drawn from the point (a,2) to the hyperbola x216−y29=1 are perpendicular, then the value of a2 is _____
View Solution
