The number of integral solutions of the inequation x+y+z≤100,(x≥2,y≥3,z≥4) , is
A
.100C2
B
.94C3
C
.93C2
D
None of these
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The graphical solution of the inequalities x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0 is
A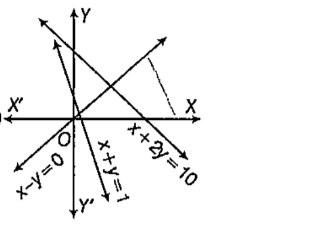 B
B C
C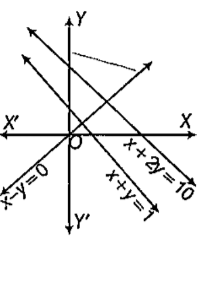 D
D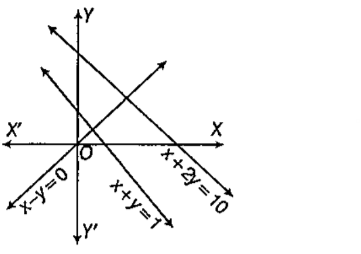
The number of integral solution of x+y+z=0 with x≥−5,y≥−5,z≥−5 is
A134B136C138D140The region represented by the solution of system of inequalities 5x+4y≤40,x≥2,y≥3 is
AboundedBunboundedCdoes not existDNone of these
3x+4y≤60,x≥2y,x≥1,y≥0
View SolutionDraw the graph of the solution set of the inequation 2x+y≥2,x−y≤1,x+2y≤8,x≥0andy≥0
View SolutionZ=3x+5y
x+y≥2,x+3y≥3x≥0,y≥0
View SolutionFor the system for linear inequations x+y≤6,3x+5y≥15,x≥0,y≥0, If Z=3x+2y, then the maximum value of Z occurs at :
View SolutionThe shaded region representing the solution set of the system of inequalities x−2y≤3,3x+4y≥12,x≥0,y≥1 in the following figure is
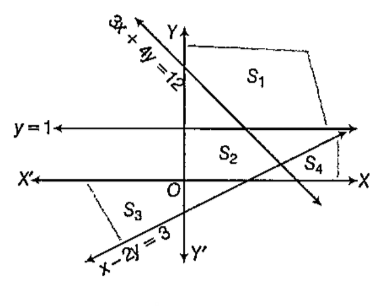
View Solution
