The linear mass density, λ(x), for a one-dimensional object of length 2x0 is plotted in the graph. The location of the center of mass for this object is rc from origin then 9rcx0 is --------------
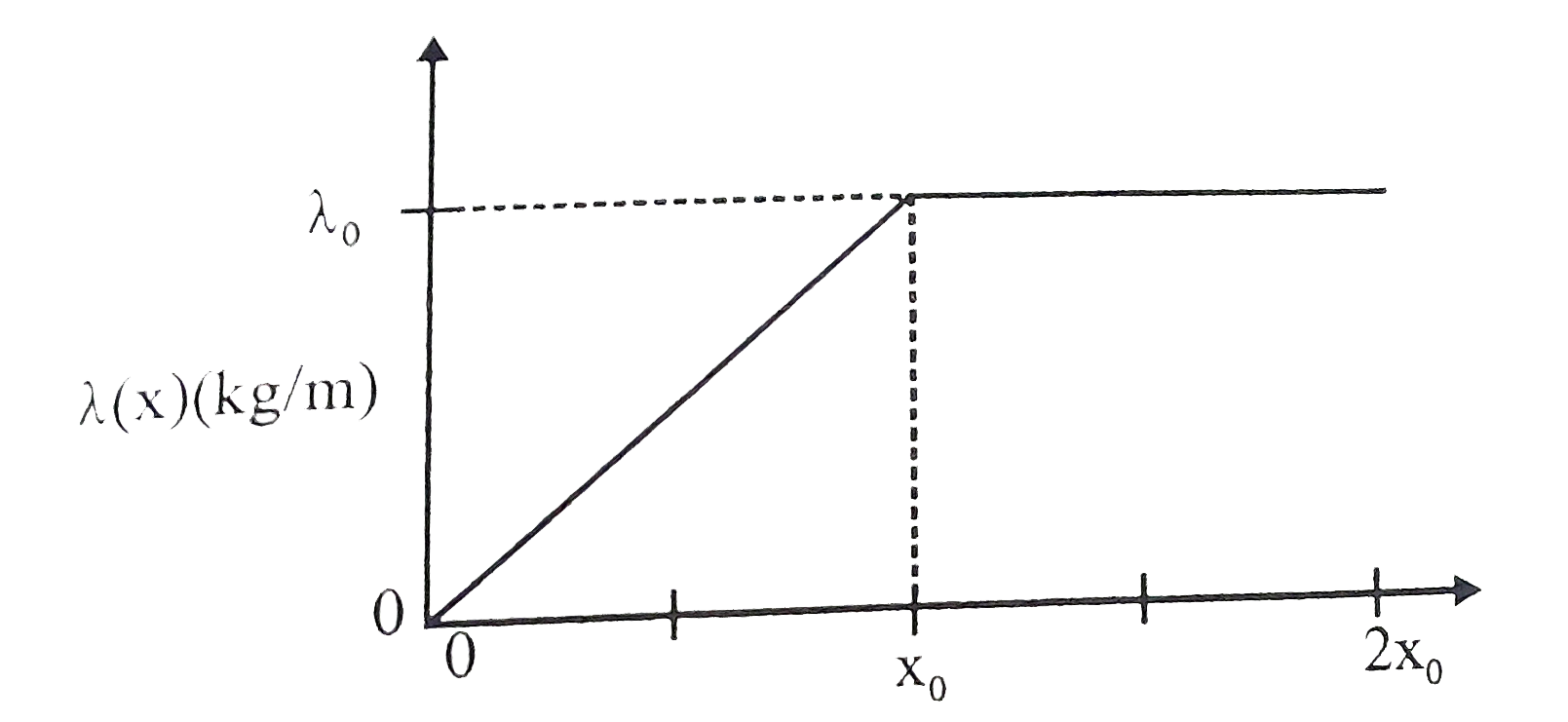
x0∫0x(λ0xx0)dx+(x0+x02)(λ,x0)λ0x02+λ0x0=11x09
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Chemistry, SECTION-2 (PART-C)10videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Mathematics, SECTION-3 (PART-C)10videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - Mathematics, SECTION-3 (PART-B) [MATRIX TYPE]2videos
TEST PAPERS
- BOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions1videos
PROBABILITY
- BOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column7videos
THERMODYNAMICS
Similar Questions
The linear mass density lambda of a rod AB is given by λ=α+βx kg/m taking O as origin. Find the location of the centre of mass from the end A?
View SolutionThe linear mass density lambda of a rod AB is given by λ=aplha+βxkgm taking O as origin. Find the location of the centre of mass from the end A?
View Solution
Knowledge Check
- Question 1 - Select One
If the linear mass density of a rod of length 3 m (lying fromy=0 toy=3m) varies as λ=(2+y)kg/m,then position of the centre of mass of the rod from y=0 is nearly at
A2mB1.7mC2.5mD2.7m - Question 2 - Select One
A point object of mass m is kept at (a, 0) along x-axis. What mass should be kept at (-3a,0), so that centre of mass lies at origin ?
AmB2mCm3D3m
If the linear mass density of a rod of length 3 m (lying fromy=0 toy=3m) varies as λ=(2+y)kg/m,then position of the centre of mass of the rod from y=0 is nearly at
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionThe liner density of a rod of length 2m varies as λ=(2+3x) kg/m, where x is distance from end A . The distance of a center of mass from the end B will be
_PHY_E05_180_Q02.png)
View SolutionA point object of mass m is kept at (a, 0) along x-axis. What mass should be kept at (-3a,0), so that centre of mass lies at origin ?
View SolutionThe density of a linear rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.
View Solution