A particle performing S.H.M . Undergoes displacement A/2 (where A= amplitude of S.H.M. ) in one second. At t=0 the particle was located at either extreme position or mean position. The time period of S.H.M. can be :( consider all possible cases )
A
12s
B
2.4 s
C
6 s
D
1.2s
Text Solution
ABCD
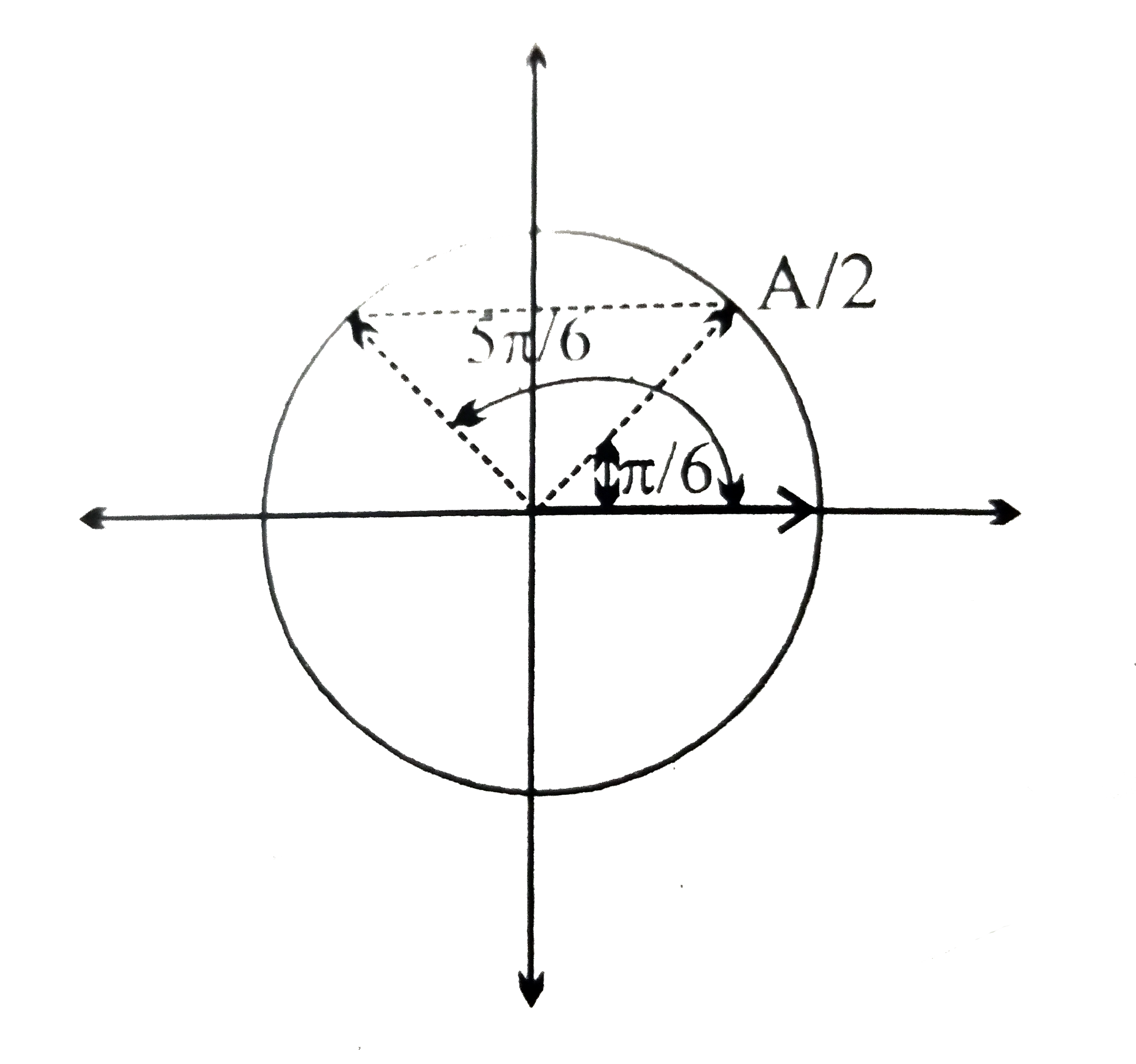
∞=θt
∞21=π/6,2πT1=π6,T1=12
∞2=5π/6,2πT2=π6,T2=2.4
T1=12sec
T2=2.4sec
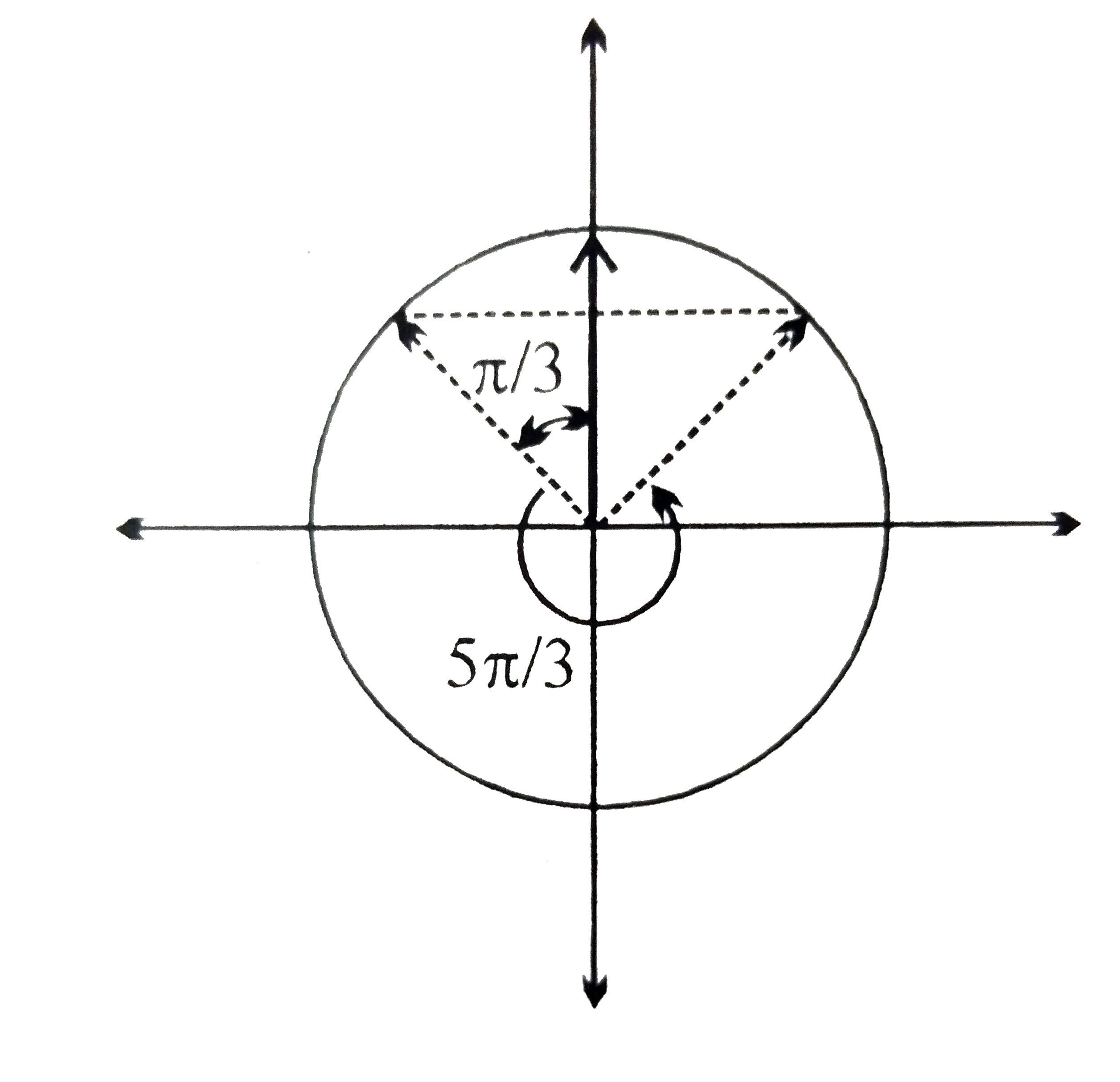
θ11=π/31,2πT11=π3,T11=6sec
θ12=5π/31,2πT12=5π3,T12=1.2sec
|
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-B [Matrix Types]
2 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 Part-A ( single correct choice type )
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION-1 Part-A (Reasoning type )
1 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
A particle performing S.H.M undergoes displacement of A/2 (where A = amplitude of S.H.M.) in one second. At t=0 be the particle was located at either position or mean position. The time period of S.H.M. can be : (consider all possible cases)
A12sB2.4C6sD1.2sThe particle performing S.H.M., about mean position it has
Amaximum acceleration and maximum velocityBminimum acceleration and maximum velocityCmaximum acceleration and minimum velocityDminimum acceleration and minimum velocityA particle performing S.H.M., its velocity when the particle moves from mean to extreme position is
Aslower initially and faster laterallyBuniformly movesCfaster initially and momentraily falls to zeroDfast moves and stop at extreme position
The velocity of the particle midway between mean and extreme position, performing S.H.M. is
View SolutionWhen a particle executing a linear S.H.M. moves from its extreme position to the mean position, its
View SolutionA particle perfoms a S.H.M. of amplitude A and period T. It the particle is half way between the mean position and the extreme position, then its speed at that point will be
View SolutionAt the mean position, the potential energy of a particle performing S.H.M. is
View SolutionA particle performs a S.H.M. and starts from the mean position. The graph of restoring force against time for the particle is a
View Solution
