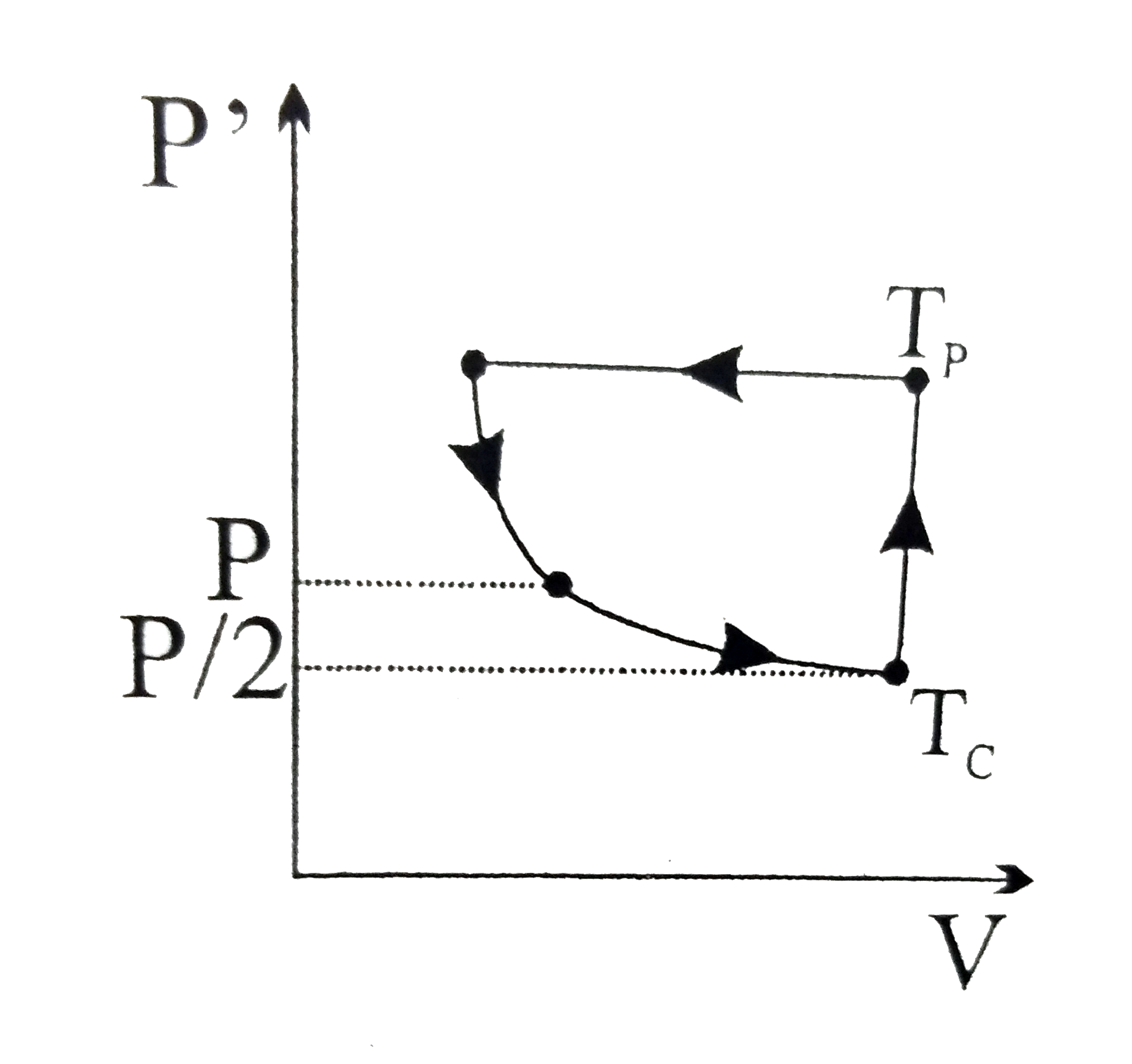
1 mole of an ideal gas , [γ=1.5], are taken through a series of process.
![1 mole of an ideal gas , [gamma=1.5], are taken through a series of process. {:(](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PT_4_P1_E02_011_Q01.png)
Information-IThe tempearature at state'A' is 300KInformation-IIThe reversible isothermal expansion form B to C doubles the volume Information-IIIThe entropy change of the system from C to D is 4 ln 16 Cal/K.
Select the correct option(s) using above information.
The entropy change of the system from D to A is =3R ln 8
The temperature at point D is 2400 K
The work done from A to B is -600 Cal.
The work done from B to C is -300 ln 2 Cal.
(A),(B),( C),(D)
ΔSCD=4ln16
=nCvRlnTDTC
TDTC=16=P'P/2
P'=8P
For AB TBTA=(PAPB)1−γγ
T(B)300=(8)−1/3=12
TB=150
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 Part-B ( Matrix type )
2 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 Part-A [ single correct choice type ]
5 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION-2 Part-A ( Reasoning type )
2 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View Solution
Knowledge Check
When 5 moles of an ideal gas is expended at 350 K reversibly from 5 L to 40 L, then the entropy change for the process is (R = 2 cal mol−1K−1)
A9.01calK−1B20.8calK−1C−15.2calK−1D22.3calK−1An ideal gas whose adiabatic exponent γ is expanded according to the law P=αV, where α isa constant the initial volume of the gas is equal to V∘. As a result of expansion, the volume increases 4 times. Select the correct option for above information.
AMolar heat capacity of gas in the process is R(γ+1)2(γ−1)BWork done by the gas is 15V2oα2CChange in internal energy of gas is 15V2oα2DBoth B and C are correct
One gm mole of an ideal gas at S.T.P is subjected to a reversible adiabatic expansion to double its volume. Find the change in internal energy in the process. Given γ=1.4[E.Q.]
View SolutionAn ideal gas (γ=1.67) is taken through the process abc shown in figure . The temperature at the point a is 300k. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
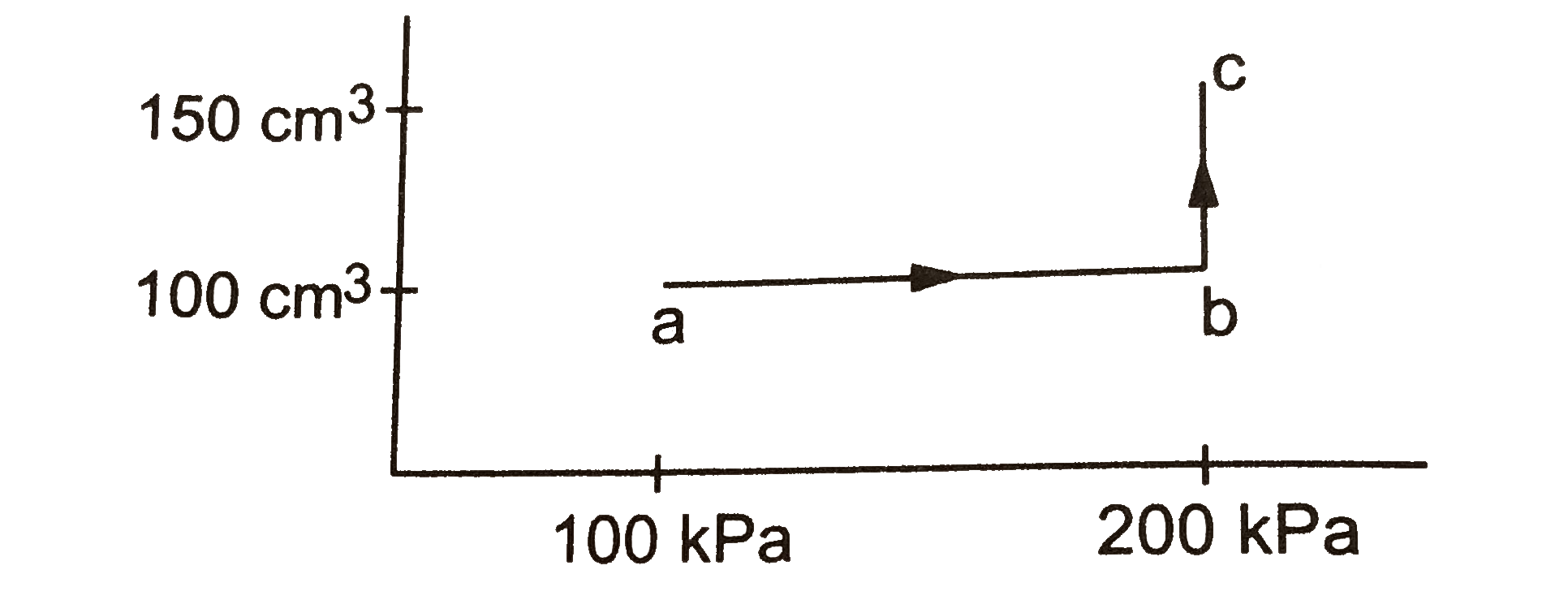
View SolutionAn ideal gas (γ=1.67) is taken through the process abc shown in figure . The temperature at the point a is 300k. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.

View SolutionWhen 5 moles of an ideal gas is expended at 350 K reversibly from 5 L to 40 L, then the entropy change for the process is (R = 2 cal mol−1K−1)
View SolutionWhen 5 moles of an ideal gas is expanded at 350 K reversibly from 5 L to 40 L, then the entropy change for the process is(R=2calmol−1K−1)
View Solution5 moles of an ideal gas expand isothermally and reversible from a pressure of 10 atm to 2 atom at 300K. What is the largest mass which can be lifted through a height of 1 metre in this expansion?
View Solution
