Consider a reversible reaction :
$A k_{1} \Leftarrow \Rightarrow k_{2} B$
Which is a first order in both the directions $(k_{1} = \frac{1.38}{3} \times 10^{- 2} {min}^{- 1})$ . The variation in concentration is plotted with time shown below.

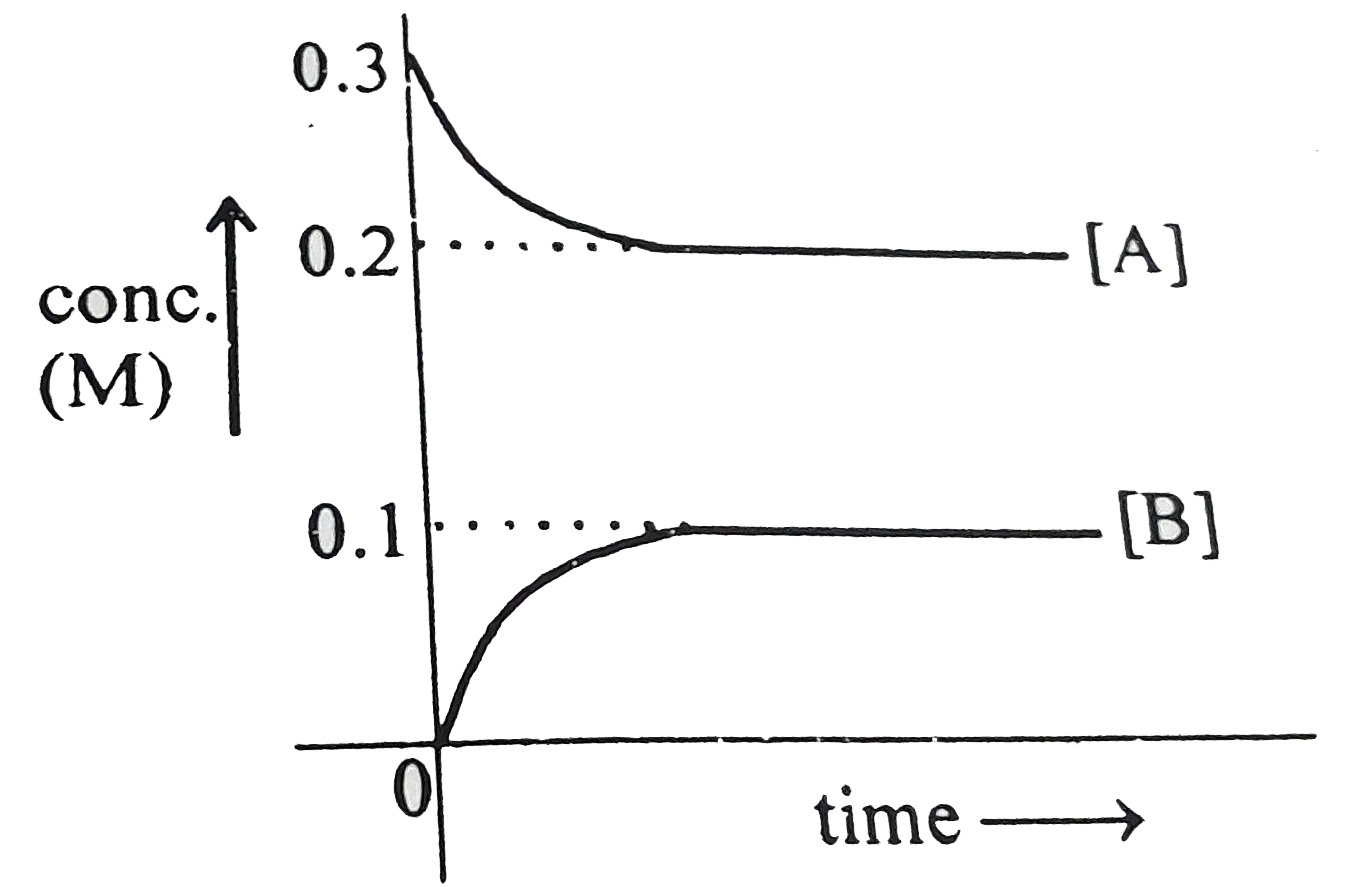
Calculate the time (in minute) at which $25 %$ of A would be exhausted. $[ln 2 = 0.69]$

Text Solution

Verified by Experts

$k_{e q} = \frac{0.1}{0.2} = \frac{1}{2} = \frac{k_{1}}{k_{2}}$
$k_{2} = \frac{2}{3} \times 1.38 \times 10^{- 2}$
$ln \frac{0.1}{0.1 - 0.075} = (k_{1} + k_{2}) t$
$2 \times 0.69 = 1.38 \times 10^{- 2} \times t$
t = 100 min. ]

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

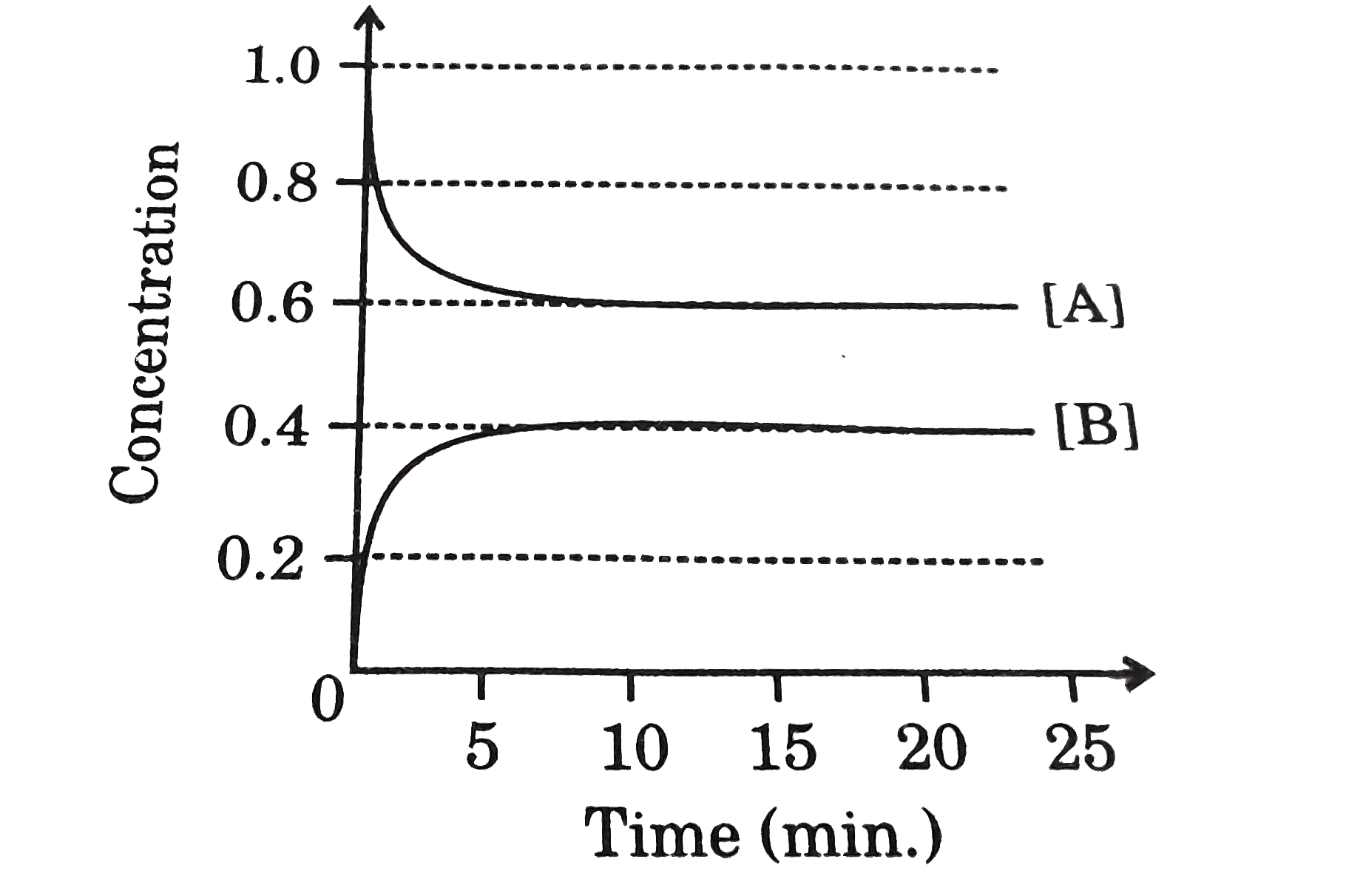
For the reversible reaction $A k_{f} \Leftarrow === \Rightarrow k_{b} B$ (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run.
Calculate [B] at time $t = \frac{1}{5}$ min.
$[Given : k_{b} = 3 {min}^{- 1} and \frac{1}{e} = 0.37]$
A0.37
B0.153
C0.2
D0.252
Question 2 - Select One or More
For a reversible reaction $A k_{1} = 4 \times 10^{2} s^{- 1} \Leftarrow ====== \Rightarrow k_{2} = 2 \times 10^{2} s^{- 1} B$ initial concentration of A is 21 mol $L^{- 1}$ . Select the correct statement:
AEquilibrium concentration of A is 14 mol $L^{- 1}$
BEquilibrium conentration of B is 14 mol $L^{- 1}$ .
CThe concentration of A reduce by 50% of equilibrium concentration after 11.55 sec .
DThe concentration of A reduce to 50% after 23.1 sec.
Question 3 - Select One
For the reversible reaction : $A o K_{1} \Leftarrow \Rightarrow K_{2} B, k_{1} = 0.02$ min"^(-1) and $k_{2} = 0.03 - 1 min$ . The reaction is stated with A only .If the half life of such reaction is defined as the time in which half of the equilibrium amount of B is formed , then , what is the half life of reaction ?
A34.65 min
B23.10 min
C13.86 min
DInfinite

BANSAL-TEST PAPERS-CHEMISTRY SECTION-2 PART-C [INTEGER TYPE]

Home
Ask Doubt
Profile