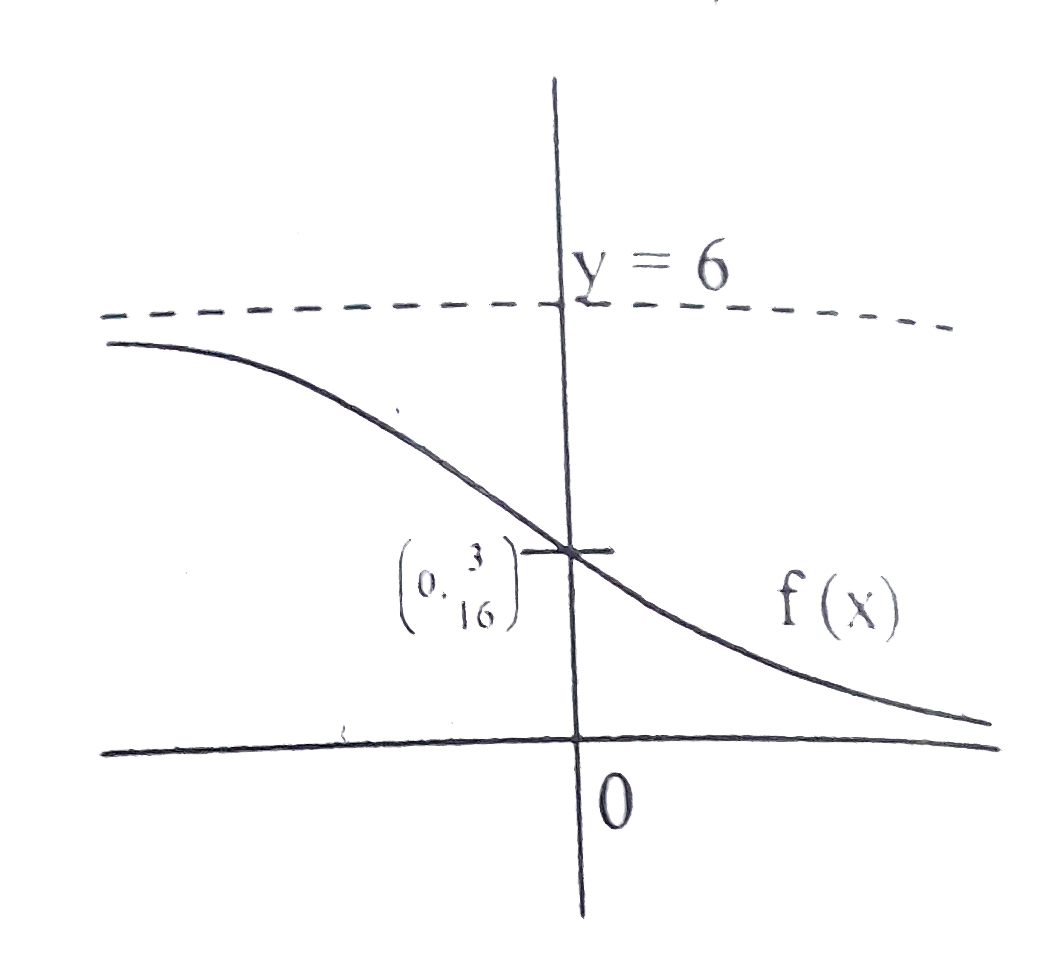
Let a function is defined as f:R→R such that f(x)=61+3lex. Find the number of different integral values which function f(x) can take ?
Text Solution
f(x) can take 1,2,3,4,5 as f(x) is continous function.
∴ Using IVT we can say that f(x) can take 5 integral value
|
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION - 1 [PARAGRAPH TYPE]
4 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION - 1 [MULTIPLE CORRECT CHOICE TYPE]
6 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 PART-B [MULTIPLE CORRECT CHOICE TYPE]
5 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Video
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
Let f be a differentiable function defined on R such that f(0) =−3. If f'(x) ≤5 for all x then
Af(2)>7Bf(2)≤7Cf(2)>8Df(2)=8If a function f:R→R is defined by f(x)=x2−5x2+4, then f is
Aone-one but not ontoBonto but not one-oneCneither one-one nor ontoDa bijectionIf f:R→R is a function defined by f(x)=x3+5 then f−1(x) is
A(x+5)13B(x−5)13C(5−x)13D5-x
Let f be a function such that f(3)=1 and f(3x)=x+f(3x−3) for all x. Then find the value of f(300).
View SolutionThe function f:R→R defined by f(x)=ex is
View SolutionLet f be a real-valued function such that f(x)+2f(2002x)=3x. Then find f(x).
View SolutionLet a function f defined from R→R as f(x)=[x+p2forx≤2andpx+5,forx>2 , If the function is surjective, then find the sum of all possible integral values of p in [−100,100].
View SolutionLet F:R→R be function defined by f(x)={x+1xx>0exx≤0 then f is
View Solution
