विद्युत- चुंबकीय प्रेरण के लिए फैराडे का नियम लिखें। दो समाक्षीय लम्बी परिनालिकाओं के बीच अन्योन्य प्रेरकत्व की गणना करें।

Video Solution

Text Solution

Verified by Experts

विधुत - चुम्बकीय प्रेरण के लिए फैराडे का नियम - प्रथम नियम - किसी चालक या कुण्डली पर पड़नेवाले चुम्बकीय फ्लक्स में परिवर्तन होने पर चालक या कुण्डली से विधुत धारा प्रेरित होती है। प्रेरित धारा तब तक प्रवाहित होती है जब तक चुम्बकीय फ्लक्स में परिवर्तन होता रहता है।
द्वितीय नियम - प्रेरित वि वा बल का परिमाण चुम्बकीय फ्लक्स में परिवर्तन की डॉ के समानुपाती होता है।
$E = - N \frac{Δ φ}{Δ t} = \frac{Δ (N φ)}{Δ t}$
जहाँ E= प्रेरित वि वा बल N= कुंडली में फेरों को संख्या
$\frac{Δ φ}{Δ t} =$ फ्लक्स के परिवर्तन की दर
यहाँ ऋणात्मक चिह्र का प्रयोग किया गया है क्योंकि प्रेरित धारा या वि वा बल चुम्बकीय फ्लक्स में परिवर्तन का विरोध करता है।
फ्लक्स में परिवर्तन तीन प्रकार के होता है -
(i) चुम्बकीय क्षेत्र B को बदलकर , (ii) क्षेत्रफल $Δ A$ को बदलकर , (iii) B और $Δ A$ को बदलकर और (iv) B और $Δ A$ के आपेक्षिक दिकविन्यास $θ$ को बदलकर। यहाँ पर प्रथम तरीके से फ्लक्स में परिवर्तन कर प्रेरित धारा उत्पन्न की जाती है।
दो लम्बी समाक्षीय परिनालिकाओं का अन्योन्य प्रेरकत्व -

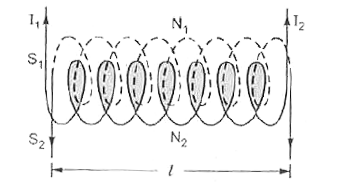
माना $S_{1} & S_{2}$ = , दो समाक्षीय परिनालिकाएँ जिसमें $S_{2}$ पूरी तरह $S_{1}$ से घिरा हुआ है।
$N_{1} & N_{2} =$ क्रमशः $S_{1}$ तथा $S_{2}$ में लपेटनों की संख्या
l = समान लम्बाई वाली परिनालिका की लम्बाई
$n_{1} = \frac{N_{1}}{l} = S_{1}$ के इकाई लम्बाई में लपेटनों की संख्या
$\Rightarrow N_{1} = n_{1} l$
$n_{2} = S_{2}$ के इकाई लम्बाई में लपेटनों की संख्या
$\Rightarrow N_{2} = n_{1} l$
Let $I_{1} = S_{1}$ में प्रवाहित धारा क मात्रा , A = अनुप्रस्थ काट का क्षेत्रफल
$∴$ परिनालिका में चुम्बकीय क्षेत्र
$B_{1} = μ_{0} n_{1} I_{1}$
$S_{1}$ परिनालिका के प्रत्येक घेरे से सम्बद्ध चुम्बकीय फ्लक्स
$ϕ . = {\to B}_{1} . \to A$
$ϕ . = {\to B}_{1} . \to A = {\to B}_{1} . A {cos 0}^{\circ} = B_{1} A = μ_{0} n_{1} I_{1} A$
$S_{2}$ परिनालिका के प्रत्येक घेरे इ सम्बद्ध चुम्बकीय फ्लक्स
$∴ ϕ_{2} = N_{2} ϕ$
$= (η_{2} l) μ_{0} n_{1} I_{1} A = [μ_{0} n_{1} n_{2} A l] I_{1}$ ...(1)
ज्ञात है , $ϕ_{2} = μ_{12} I_{1}$ ...(2)
समी (1) तथा (2) , की तुलना से ,
$M_{12} = [μ_{0} n_{1} n_{2} A l]$
= अन्योन्य प्रेरण जब धारा $S_{2}$ से प्रवाहित होती है जिससे
$S_{1}$ में चुम्बकीय फ्लक्स उत्पन्न होता है
सामान्यत : $M_{12} = M_{21} = M \Rightarrow M = μ_{0} η_{1} η_{2} A l$
$\Rightarrow M = μ_{0} \frac{N_{1}}{l} \times \frac{N_{2}}{l} \times A \times l$
यह अन्योन्य प्रेरण का अभीष्ट व्यंजक है।

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION PAPER 2019

Topper's Solved these Questions

Similar Questions

JHARKHAND BOARD PREVIOUS YEAR PAPERS-QUESTION PAPER 2019-2019

Home
Ask Doubt
Profile