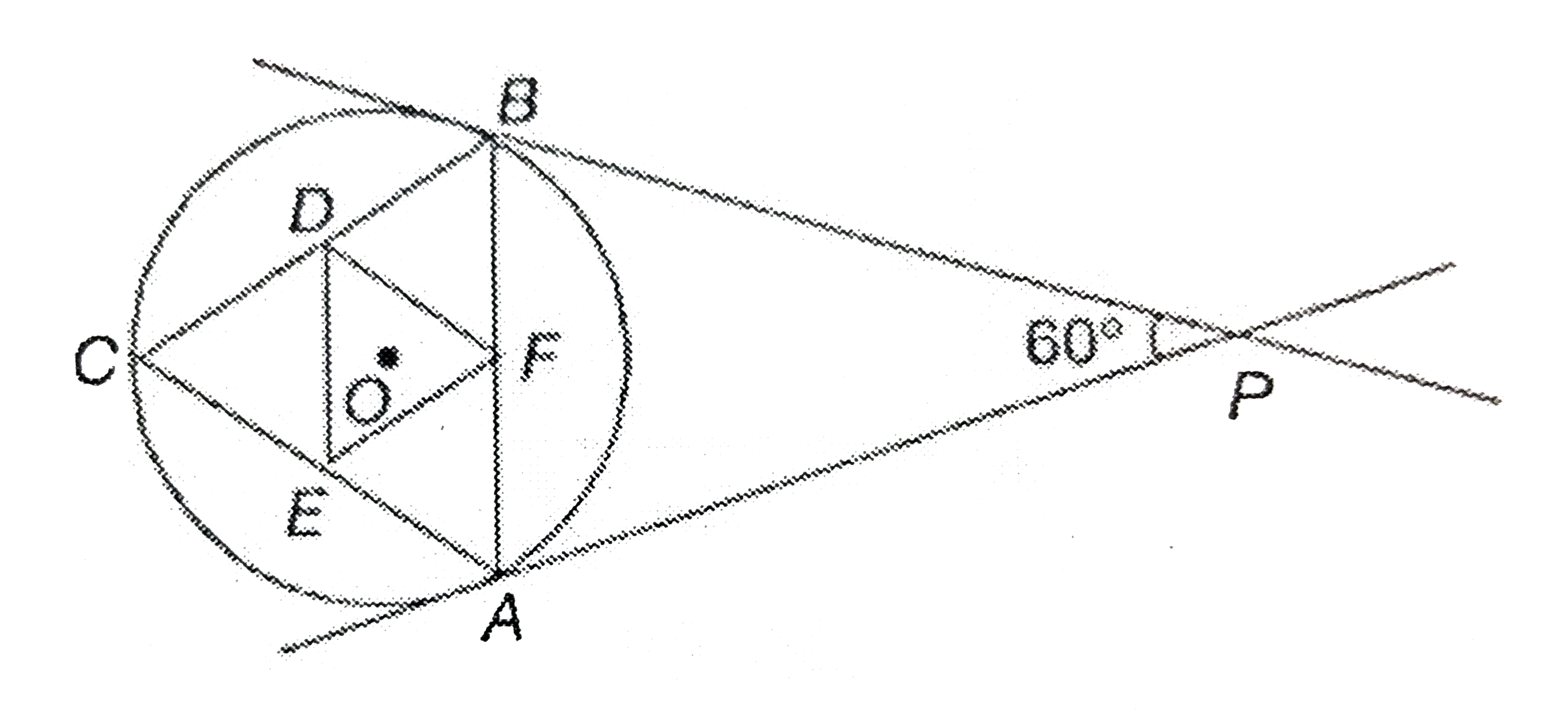
In the diagram given above,D,E and F are mid-points of BC, CA and AB . If the angle between the tangents drawn at A and B is 60∘ , find ∠EFD.
The correct Answer is:60∘
Step by step video & image solution for In the diagram given above,D,E and F are mid-points of BC, CA and AB . If the angle between the tangents drawn at A and B is 60^@ , find angle EFD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -1
34 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -2
17 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Short answer type questions
13 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
In the diagram given above, D,EandF are midpoints of BC,CAandAB. If the angle between the tangents drawn at AandB is 60∘, find ∠EFD.
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View Solution
Knowledge Check
D,E,F are the mid points of BC,CAandAB of ΔABC. If ADandBE intersect in G, then AG+BG+CG is equal to
AAD=BE=CFB23(AD+BE+CF)C32(AD+BE+CF)D13(AD+BE+CF)
D, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View Solution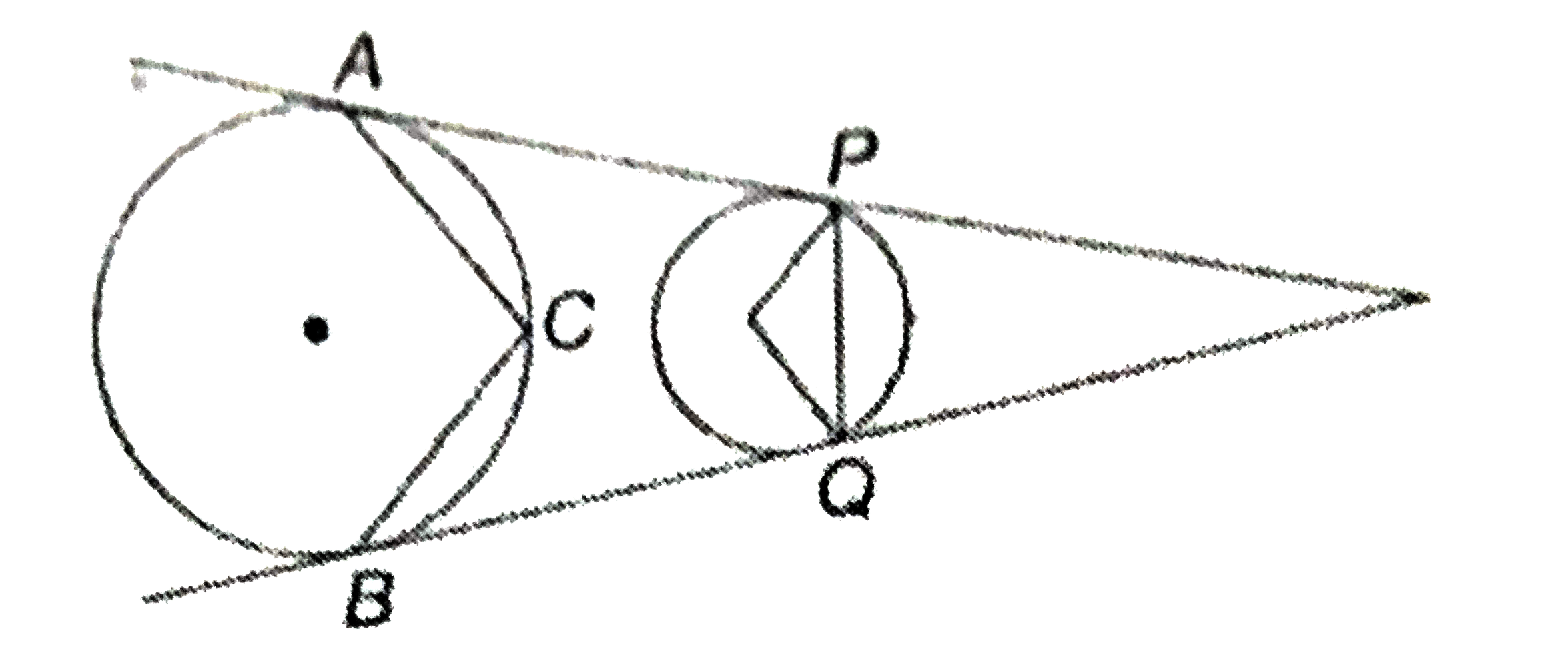
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIn the diagram above, A,B,PandQ are points of contacts of direct common tangents of the two cir-cles. If ∠ACB is 120∘, then find the angle between the two tangents and angle made by PQ at thecentre of same circle.
View SolutionIf three points are A(−2,1)B(2,3),andC(−2,−4) , then find the angle between ABandBC.
View Solution
