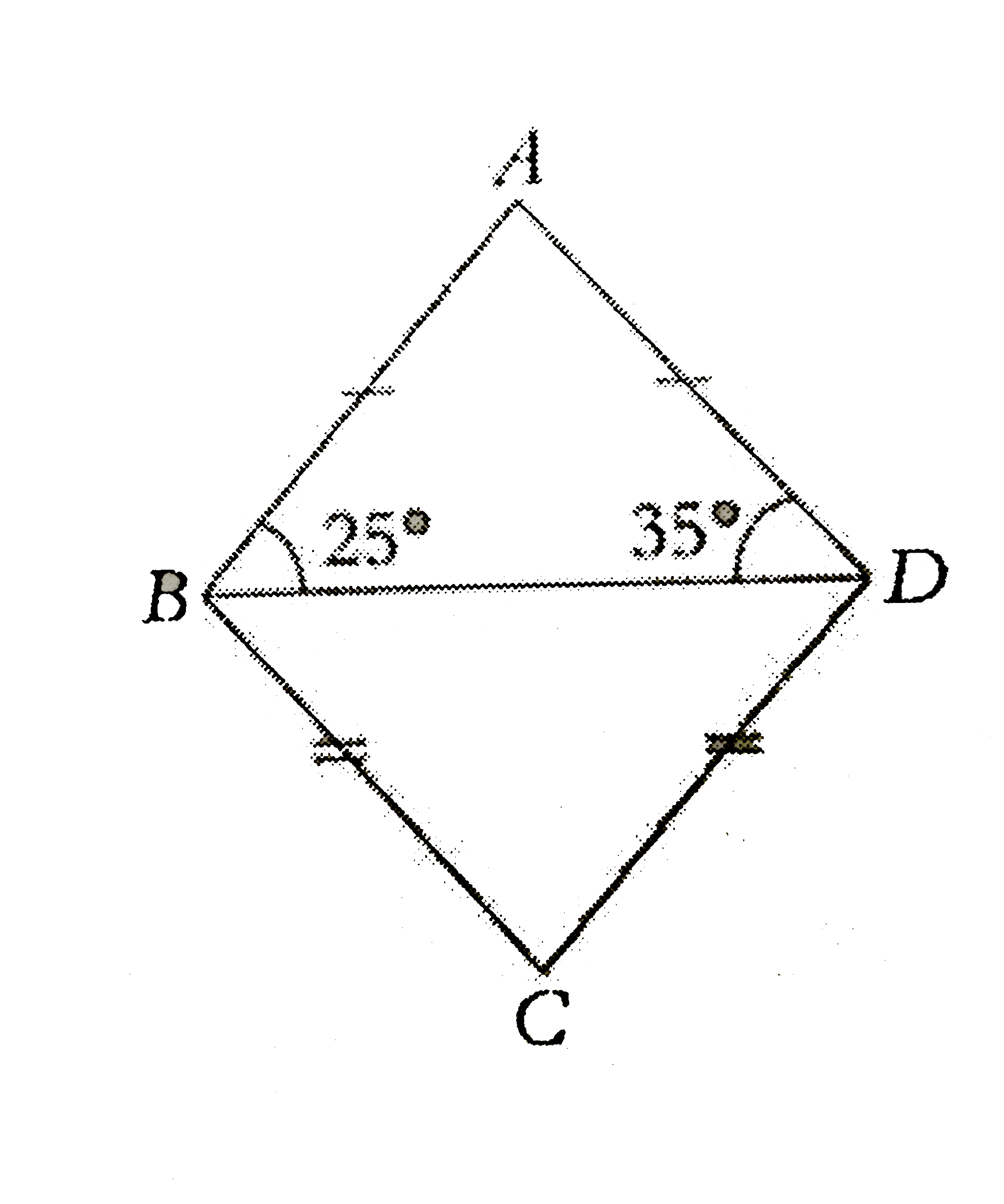
ABCD is a kite in which AB=AD and CB=CD. If ∠ABD=25∘and∠BDC=35∘, then find ∠A−∠C.
Video Solution
Text Solution
Given ∠ABD=25∘andanl≥BDC=35∘.
In ΔBCD,BC=CD.
⇒∠CDB=∠CBD⇒∠CBD=35∘
⇒∠C=180∘−(35∘+35∘)=110∘
AB=AD
Also given,
⇒∠ABD=∠ADB⇒∠ADB=25∘
∠A=180∘−(25∘+25∘)=130∘
Now,
∴∠A−∠C=130∘−110∘=20∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very Short answer Type Question25videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short answer Type Question29videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)8videos
FORMULAS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -212videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a △ABC,∠A=35∘ and ∠B=65∘,find the measure of ∠C
A80∘B120∘C155∘D140∘ - Question 2 - Select One
ABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about
 Athe diagonal ACBthe diagonal BDCnone of theseDboth (a) and (d)
Athe diagonal ACBthe diagonal BDCnone of theseDboth (a) and (d) - Question 3 - Select One
In the given figreu AB∣∣CD,∠BAD=30∘and∠ECD=50∘, find ∠CED
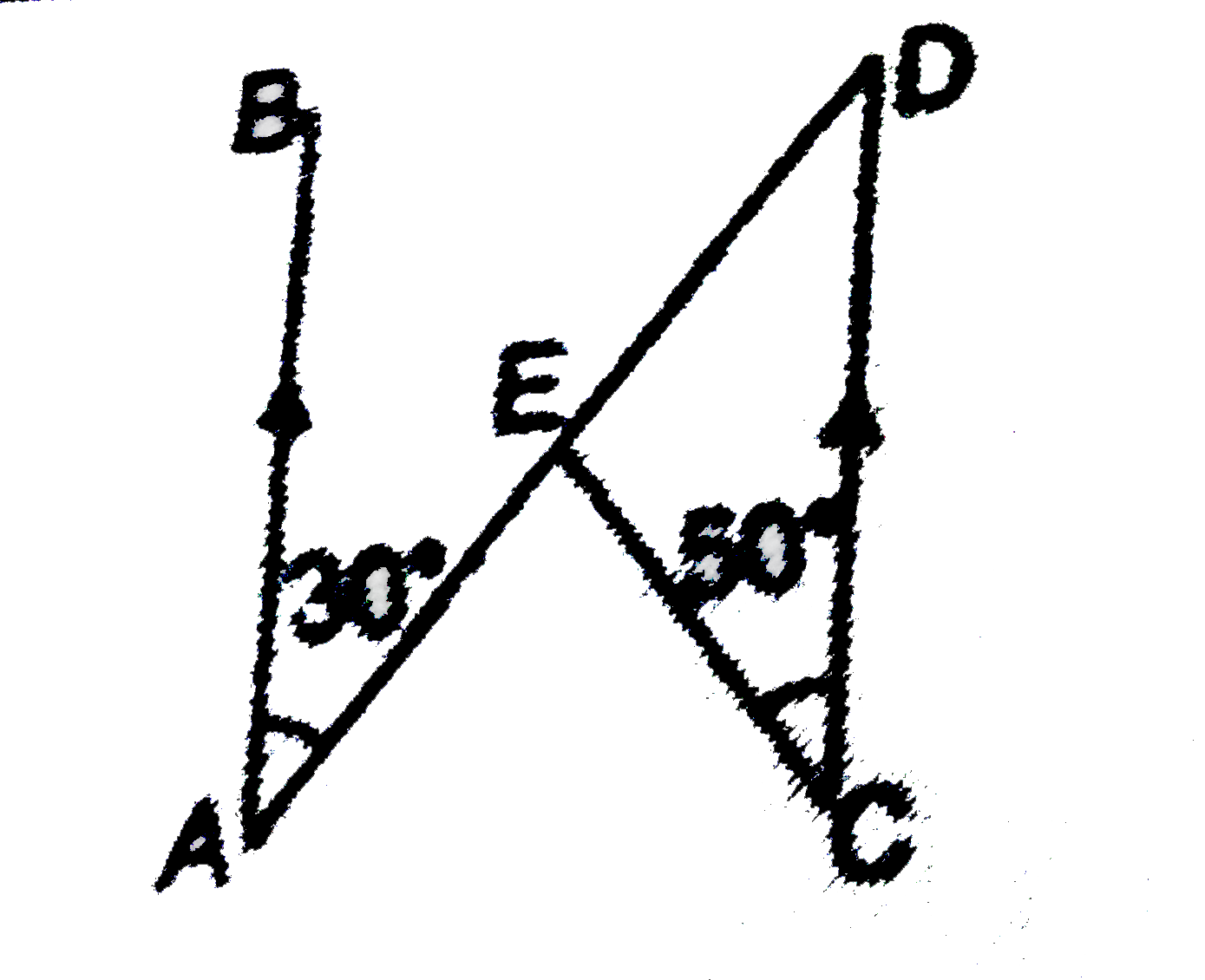 A120∘B30∘C100∘D50∘
A120∘B30∘C100∘D50∘
ABCD is a kite in which AB=AD and CB=CD. If ∠ABD=30∘and∠BDC=40∘, then find ∠A+∠C.
View SolutionABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about
 View Solution
View SolutionIn parallelogram ABCD, if ∠A=(7x+40)∘ and ∠C=(2x+80)∘ , then find ∠A .
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionIn △ABC,AB=10cm,∠A=45∘ and ∠C=60∘. Find BC.
View Solution

