For each of the exercises given below, verify that the given function ( implicit or explicit ) is a solution of the corresponding differential equation.
y=aex+be−x+x2:
x(d2y)+2dydx−xy+x2−2=0Solution in Tamil
Step by step video & image solution for For each of the exercises given below, verify that the given function ( implicit or explicit ) is a solution of the corresponding differential equation. y=ae^(x)+be^(-x)+x^(2): x(d^(2)y)+2(dy)/(dx)-xy+x^(2)-2=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - UNIT TEST
8 Videos
- DIFFERENTIAL EQUATIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - CONTINUOUS EVALUATION (ASSIGNMENT)
1 Videos
- DIFFERENTIAL EQUATIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Additional question for practice 9.6
4 Videos
- CONIC SECTIONS BOOK - NEW JOYTHI PUBLICATIONCHAPTER - CONIC SECTIONS EXERCISE - EXERCISE - HYPERBOLA
9 Videos
- INTEGRALS BOOK - NEW JOYTHI PUBLICATIONCHAPTER - INTEGRALS EXERCISE - OBJECTIVE TYPE QUESTIONS
34 Videos
Similar Questions
Find the order and degree of the differential equation t2d2sdt2−stdsdt=s
View SolutionComplete the following tables
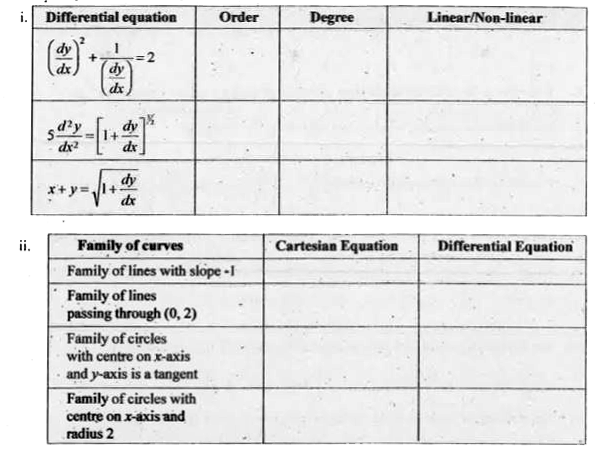
View SolutionFind the general solution of the following differential equation.
dydx+y=e−x
View SolutionThe vertices of the hyperbola 9x2−16y2=144
View Solution∫ealogxdx is equal to
View SolutionVerify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:y=√1+x2 : y'=xy1+x2
View SolutionFor each of the exercises given below, verify that the given function ( implicit or explicit ) is a solution of the corresponding differential equation.
y=ex(acosx+bsinx):
d2ydx2−2dydx+2y=0
View SolutionFor each of the exercises given below, verify that the given function ( implicit or explicit ) is a solution of the corresponding differential equation. x^(2)=2y^(2)logy:(x^(2)+y^(2))(dy)/(dx)-xy=0
View SolutionFor each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) xy=aex+be−x+x2:xd2ydx2+2dydx−xy+x2−2=0
(ii) y=ex(acosx+bsinx):d2ydx2−2dydx+2y=0
(iii) y=xsin3x:d2ydx2+9y−6cos3x=0
(iv) x2=2y2logy:(x2+y2dydx−xy=0
View SolutionVerify that the given function (Explicit Or Implicit) is a solution of the corresponding differential equation y=√1+x2:y'=xy1+x2
View SolutionVerify that the given function (Explicit Or Implicit) is a solution of the corresponding differential equation y=√a2−x2x∈(−a,a):x+ydydx=0(y≠0)
View SolutionFor each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) xy=aex+be−x+x2:xd2ydx2+2dydx−xy+x2−2=0
(ii) y=ex(acosx+bsinx):d2ydx2−2dydx+2y=0
(iii) y=xsin3x:d2ydx2+9y−6cos3x=0
(iv) x2=2y2logy:(x2+y2dydx−xy=0
View SolutionVerify that the given functions ( explicit or implicit ) is a solution of the corresponding differential equation y=√1+x2:y'=xy1+x2
View SolutionFor each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
xy=aex+be−x+x2:xd2ydx2+2dydx−xy+x2−2=0
View SolutionFor each of the exercises given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.
(i) xy=aex+be−x+x2:xd2ydx2+2dydx−xy+x2−2=0
(ii) y=ex(acosx+bsinx):d2ydx2−2dydx+2y=0
(iii) y=xsin3x:d2ydx2+9y−6cos3x=0
(iv) x2=2y2logy:(x2+y2dydx−xy=0
View Solution
