Evaluate the product (3→a+5→b).(2→a+7→b).Solution in Tamil
Step by step video, text & image solution for Evaluate the product (3 vec a + 5 vec b).(2 vec a + 7 vec b). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.412videos
VECTOR ALGEBRA
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.12videos
VECTOR ALGEBRA
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.219videos
VECTOR ALGEBRA
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS134videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find ∣∣→a×→b∣∣ if →a=ˆi−7ˆj+7ˆk and →b=3ˆi−2ˆj+2ˆk.
03:46View SolutionIn the figure which vectors are
(i) equal (ii) collinear (iii) coinitial
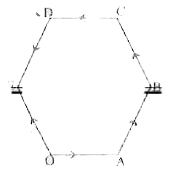 04:40View Solution
04:40View SolutionCompute the magnitude of the following vectors.
→a=ˆi+ˆj+ˆk, →b=2ˆi−7ˆj−3ˆk04:19View SolutionIf A+B+C=90∘ then
cotA+cotB+cotCcotAcotBcotC =01:58View SolutionVector →a,→b and →c are such that →a+→b+→c=→0 and |a|=3,∣∣→b∣∣=5 and |→c|=7. Find the angle between →a and →b .
02:55View SolutionIf →a+→b+→c=→0, −→|a|=3, ∣∣→b∣∣=5 and |→c|=7.
Find the angle betweeen →a and →b02:21View Solutionvec a + vec b + vec c = vec 0, | vec a | = 3, | vec b | = 5, | vec c | = 7 then angle between vec a and vec b is
02:07View SolutionIf →a,→band→c be three vectors such that →a+→b+→c=0 and |→a|=3,∣∣→b∣∣=5,∣∣→C∣∣=7, find the angle between →a and →b.
02:28View SolutionIf →a+→b+→c=0 and|→a|=3,∣∣→b∣∣=5,|→c|=7, then find the value of →a,→b+→b.→c+→c.→a.
01:44View Solution→a+→b+→c=→0 such that |→a|=3,∣∣→b∣∣=5and|→c|=7.
What is →a.→b+→b.→c+→c.→a equal to ?01:58View Solution→a+→b+→c=→0 such that |→a|=3,∣∣→b∣∣=5and|→c|=7.
What is ∣∣→a+→b∣∣ equal to ?04:05View SolutionIf →a and →b are perpendicular vectors, ∣∣→a+→b∣∣=3 and |→a|=5, find the value of ∣∣→b∣∣.
02:34View SolutionFind |→a| and ∣∣→b∣∣, if (→a+→b).(→a−→b)=7 and |→a|=7∣∣→b∣∣
04:17View SolutionFind |→a| and ∣∣→b∣∣ if (→a+→b).(→a−→b)=3 and 2∣∣→b∣∣=|→a|.
04:08View SolutionVector →a,→b and →c are such that →a+→b+→c=→0 and |a|=3,∣∣→b∣∣=5 and |→c|=7. Find the angle between →a and →b .
03:43View SolutionIf →a+→b+→c=0 and|→a|=3,∣∣→b∣∣=5,|→c|=7, then find the value of →a⋅→b+→b⋅→c+→c⋅→a.
03:57View Solution

