Compare the velocities of the wave forms given below, and choose the correct option.

where VA,VB,VC and VD are velocities given in (A), (B), (C) and (D), respectively.
VA>VB>VC
VA<VB<VC
VA=VB=VD=VC
VA>VB=VD>VC
The correct Answer is:C
VA=VB=VD=VC
Topper's Solved these Questions
- WAVES BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Textual Evaluation Solved (Short Answer Questions )
15 Videos
- WAVES BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Textual Evaluation Solved (Long Answer Questions )
16 Videos
- WAVES BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Additional Questions Solved (Numerical Problems )
10 Videos
- SOLVED PAPER 17 (UNSOLVED)BOOK - FULL MARKSCHAPTER - SOLVED PAPER 17 (UNSOLVED)EXERCISE - Part-IV
10 Videos
- WORK, ENERGY AND POWERBOOK - FULL MARKSCHAPTER - WORK, ENERGY AND POWEREXERCISE - Additional Question Solved (Numercials)
11 Videos
Similar Questions
In the given circuit find the |VA−VB| where VA,VB are electric potentials at the points A and B.

View SolutionFigure shows four points A, B, C and D in uniform electric field →E. The line AB and CD are perpendicular and BC and AD are parallel to the field lines. If VA,VB,VCandVD are electric potential at A, B,C,D choose the correct option.
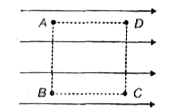
View Solution
Knowledge Check
If Vg,VwandVd represent the velocities of light in glass , water and diamond respectively , then
AVg<Vd<VwBVw>Vg>VdCVd>Vg>VwDVw<Vg<VdFigure shows four points A, B, C and D in uniform electric field →E. The line AB and CD are perpendicular and BC and AD are parallel to the field lines. If VA,VB,VCandVD are electric potential at A, B,C,D choose the correct option.
 AVA=VB=VC=VDB(VA=VB)>(VC=VD)C(VA=VB)<(VC=VD)DVA>VB=VC>VD
AVA=VB=VC=VDB(VA=VB)>(VC=VD)C(VA=VB)<(VC=VD)DVA>VB=VC>VDIf orbit velocity of planet is given by v=GaMbRc, then
Aa=13,b=13,c=−13Ba=13,b=12,c=−12Ca=12,b=−12,c=12Da=12,b=−12,c=−12
If orbit velocity of planet is given by v=GaMbRc, then
View SolutionThe velocity of a body is given by v=At2+Bt+C. If v and t are expressed in SI, what are the units of A,B and C?
View SolutionIf the orbital velocity of a planet is given by v=GaMbRc then
View SolutionThe velocity v of a particle at time t is given by v=at+bt+c , where a, b and c are constants. The dimensions of a, b and c are respectively:-
View SolutionThe amplitude of velocity of a particle is given by, Vm=V0/(aω2−bω+c) where V0, a, b and c are positive :
The condition for a single resonant frequency is
View Solution
