Calculate the resultant capacitances for each of the following combinations of capacitors .
Solution in Tamil

Video Solution

Text Solution

Verified by Experts

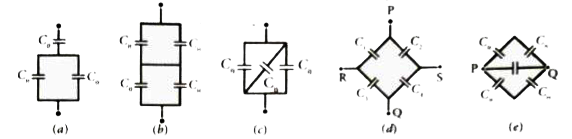
Parallel combination of capacitor 1 and 2
$C_{p} = C_{0} + C_{0} = 2 C_{0}$
Series combination of capacitor $C_{p}$ and 3
$\frac{1}{C_{s}} = \frac{1}{C_{p}} + \frac{1}{C_{3}} = \frac{1}{2 C_{0}} + \frac{1}{C_{0}} (or) \frac{1}{C_{s}} = \frac{3}{2} C_{0} (or) C_{s} = \frac{2}{3} C_{0}$
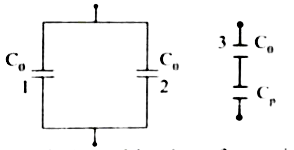
(b)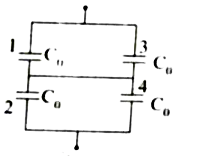
Capacitor 1 and 2 are series combination
$\frac{1}{C_{s_{1}}} = \frac{1}{C_{1}} + \frac{1}{C_{2}} = \frac{1}{C_{0}} + \frac{1}{C_{0}} = \frac{1}{C_{0}} (or) \frac{1}{C_{s_{1}}} = \frac{2}{C_{0}} (or) C_{s_{1}} = \frac{C_{0}}{2}$
Similarly 3 and 4 are series combination
$\frac{1}{C_{s_{1}}} = \frac{1}{C_{3}} + \frac{1}{C_{4}} + \frac{1}{C_{0}} + \frac{1}{C_{0}} = \frac{2}{C_{0}} (or) C_{s_{2}} = \frac{C_{0}}{2}$
$C_{s_{1}}$ and $C_{s_{2}}$ are in parallel combination

$C_{P} = C_{s_{1}} + C_{s_{2}} = \frac{C_{0}}{2} + \frac{C_{0}}{2} (or) C_{P} = \frac{2 C_{0}}{2} C_{P} = C_{0}$
(c ) Capacitor 1,2 and 3 are in parallel combination
$C_{P} = C_{0} + C_{0} + C_{0} = 3 C_{0}$
$C_{P} = 3 C_{0}$
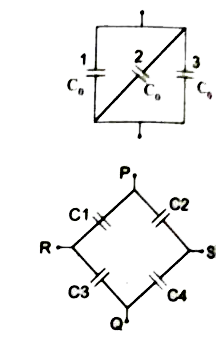
(d) Capacitar $C_{1}$ and $C_{2}$ are in combination
$\frac{1}{C_{s_{1}}} = \frac{C_{1} + C_{2}}{C_{1} C_{2}}$
$C_{s_{1}} = \frac{C_{1} C_{2}}{C_{1} + C_{2}}$

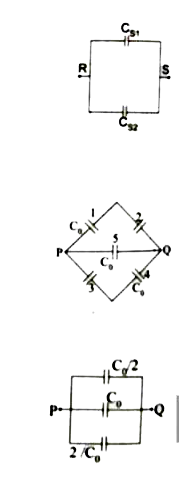
Similarly $C_{3}$ and $C_{4}$ are in series combination
$\frac{1}{C_{s_{2}}} = \frac{1}{C_{3}} + \frac{1}{C_{4}} = \frac{C_{3} + C_{4}}{C_{3} C_{4}}$
$C_{s_{2}} = \frac{C_{3} C_{4}}{C_{3} + C_{4}}$
$C_{s_{1}}$ and $C_{s_{2}}$ are in parallel combination across R.S:
$C P = C_{s_{1}} + C_{s_{2}}$
$= \frac{C_{1} C_{2}}{C_{1} + C_{2}} + \frac{C_{3} C_{4}}{C_{3} + C_{4}} = \frac{C_{1} C_{2} (C_{3} + C_{4}) + C_{3} C_{4} (C_{1} + C_{2})}{(C_{1} + C_{2}) (C_{3} + C_{4})}$
$C_{P} = \frac{C_{1} C_{2} C_{3} + C_{1} C_{2} C_{4} + C_{3} C_{4} C_{1} + C_{3} C_{4} C_{2}}{(C_{1} + C_{2}) (C_{3} + C_{4})}$
(e) Capacitor 1 and 2 are series combination
$\frac{1}{C_{s_{1}}} = \frac{1}{C_{1}} + \frac{1}{C_{2}} = \frac{1}{C_{0}} + \frac{1}{C_{0}} = \frac{1}{C_{0}}$
$\frac{1}{C_{s_{1}}} = \frac{2}{C_{0}} (or) C_{s_{1}} = \frac{C_{0}}{2}$
Similarly 3 and 4 are series combination
$\frac{1}{C_{s_{2}} = \frac{2}{C_{0}} (or) C_{s_{2}} = \frac{C_{0}}{2}}$
Three capacitors are in parallel combination

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

FULL MARKS-ELECTROSTATICS -EXERCISES

Home
Ask Doubt
Profile