Show the time period of oscillation when a bar magnet is kept in a uniform magnetic field is T = 2π√lpmB . In second, where I represents moment of inertia of the bar magnet, pm is the magnetic moment and is the magnetic field. Solution in Tamil
The magnitude of deflecting torque ( the torque which makes the object rotate ) acting on the bar magnet which will tend to align the bar magnet parallel to the direction of the uniform magnetic field →B is
|→τ|=pmBsinθ
The magnitude of restoring torque acting on the bar magnet can be written as
|→τ|=Id2θdt2
Under equilibrium conditions, both magnitude of deflecting torque and restoring torque will be equal but act in the opposite directions, which means
Id2θdt2=−pm B sin θ
the negative sign implies that both are in opposite directions. the above equation can be written as
d2θdt2=−pmBIsinθ
this is non-linear second order homogeneous differential equation. In order to make it linear. we use small angle approximation. i.e., sin θ≈θ , we get
d2θdt2=−pmBIθ
this inear second order homogeneous differential equation is a simple Harmonic differential equation. therefore,
comparing with simple Harmonic Motion (SHM) differential equation d2xdt2=−ω2x where ω is the angular frequency of the osxillation .
ω2=pmBI⇒ω=√pmBI
T = 2π√IpmB
T = 2π√IpmBH in second
where, BH is the horizontal component of Earth.s magnetic field.
Topper's Solved these Questions
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - TEXT EVALUATION SOLVED
15 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - TEXT EVALUATION SOLVED -SHORT ANSWER QUESTIONS
10 Videos
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - ADDITIONAL QUESTIONS SOLVED ( VII. NUMERICAL PROBLEMS )
5 Videos
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - ADDITIONAL QUESITON - II ADDITIONAL PROBLEMS:
11 Videos
Similar Questions
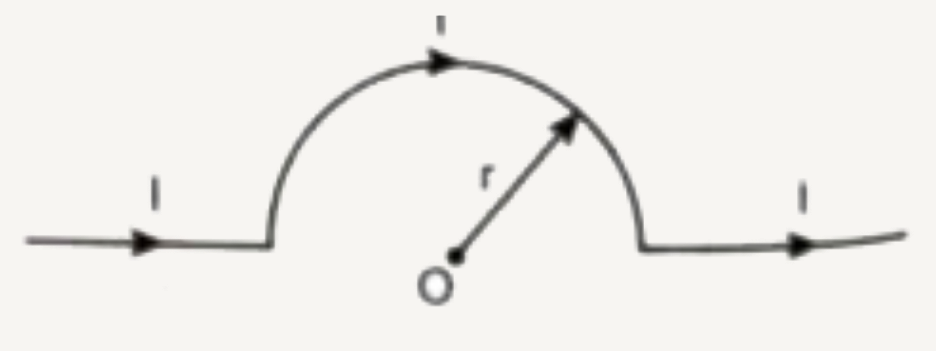
The magnetic field at the center O of the following current loop is ............ .
View SolutionWhat is meant by magnetic induction ?
View SolutionElectrons are caused to fall through a potential difference of 1500 volts. If they were initially at rest. Then calculate their final speed.
View SolutionLight from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm ). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
View SolutionA short bar magnet is kept in uniform magnetic field of 0.16 T such that dipole moment vector is at angle 30∘ with the field . The torque acting on the bar magnet is 0.032 N m . What is the magnitude of magnetic dipole moment of the magnet ?
View SolutionIf a bar magnet of magnetic moment M is kept in a uniform magnetic field B, its time period of oscillation is T. The another magnet of same length and breath is kept in a same magnetic field. If magnetic moment of new magnet is M//4 , then its oscillation time period is
View Solutionएकसमान चुम्बकीय क्षेत्र H में स्वतंत्र रूप से लटकाये गये चुंबकीय द्विध्रुक आघूर्ण M वाले लघु दंड चुम्बक का दोलन काल होगा :
View SolutionThe torque acting on a bar magnet of magnetic moment M in a uniform magnetic field B will be
View SolutionA bar magnet of moment of inertia 49xx10^(-2)kg-m^(2) vibrates in a magnetic field of induction 0.5xx10^(-4) T. The time period of vibration is 8.8s. The magnetic moment of the bar magnet is
View SolutionA short bar magnet is kept in uniform magnetic field of 0.16T such that dipole moment vecotor is at angle 30∘ with the field. The torque acting on the bar magnet is 0.032 N m. What is magnitude of magnetic dipole moment of the magnet ?
View SolutionShow the time period of oscillation when a bar magnet is kept in a uniform magnetic field is T = 2π√lpmB . In second, where I represents moment of inertia of the bar magnet, pm is the magnetic moment and is the magnetic field.
View SolutionTime period of a bar magnet oscillating in earth's magnetic field is T. Its magnetic moment is M. Now, a bar magnet of magnetic moment 2M is brought near it. The new time period will be
View SolutionShow that the time period (T) of oscillations of a freely suspended magnetic dipole of magnetic moment (m) in a uniform magnetic field (B) is given by T=2 pi sqrt((I)/(mB)) , where I is moment of inertia of the magnetic dipole.
View SolutionWrite the equation of periodic time for oscillating bar magnet in uniform magnetic field.
View SolutionIf a bar magnet of magnetic moment M is kept in a uniform magnetic field B, its time period of oscillation is T. In the same magnetic field, the time period of another magnet of same dimension and same mass but of moment M/4 is.
View Solution
