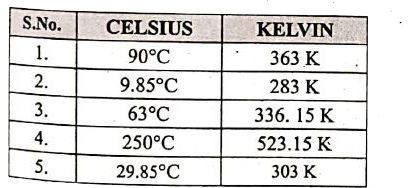
Complete the following table:
S.NO.CELSIUSKELVIN190∘C363K2?283K363∘C?4250∘C?5?303K
Text Solution
|
Topper's Solved these Questions
- MATTER AROUND USBOOK - FULL MARKSCHAPTER - MATTER AROUND USEXERCISE - ADDITIONAL QUESTION (ANSWER THE FOLLOWING IN DETAIL)
5 Videos
- MATTER AROUND USBOOK - FULL MARKSCHAPTER - MATTER AROUND USEXERCISE - ADDITIONAL QUESTION (STATE WHICH THE FOLLOWING STATEMENTS ARE TRUE OR FALSE. If false give the correct statement)
7 Videos
- CHEMICAL BONDINGBOOK - FULL MARKSCHAPTER - CHEMICAL BONDINGEXERCISE - Additional Questions (I. Long answers questions)
3 Videos
- PERIODIC CLASSIFICATION OF ELEMENTSBOOK - FULL MARKSCHAPTER - PERIODIC CLASSIFICATION OF ELEMENTSEXERCISE - ADDITIONAL QUESTIONS- LONG ANSWER QUESTIONS
4 Videos
Similar Questions
Knowledge Check
If n is a positive integer and Ck=nCk, then the value of n∑k=1k3(CkCk−1)2 is :
An+(n+2)(n+1)212Bn+(n+1)(n+2)212Cn+(n+2)(n+1)12DNone of theseIf n is a positive integer and Ck=nCk, then the value of n∑k=1k3(CkCk−1)2 is :
An12(n+1)(n+2)Bn12(n+1)2(n+2)Cn12(n+1)(n+2)2Dnone of these
If Kc is not numerically equal to Kp, how can both of the following equations be valid?
ΔGɵ=−2.303RTlogKc,ΔGɵ=−2.303RTlogKp
View SolutionIf n is a positive integer and Ck=.nCk then find the value of n∑k=1k3⋅(CkCk−1)2.
View SolutionIf Kc is not numerically equal to Kp, how can both of the following equations be valid?
ΔGɵ=−2.303RTlogKc,ΔGɵ=−2.303RTlogKp
View SolutionIf n and k are positive integers, show that 2k(.nC0)(.nCk)−2k−1(.nC1)(.n−1Ck−1)+2k−2(.nC2)((n−2k−2)).−...+(−1)k(^nCk)+(.n−kC0)=(.nCk)where(.nCk) stands for .nCk.
View SolutionGiven (1−x3)n=n∑k=0akxk(1−x)3n−2k then the value of 3⋅ak−1+ak is (a) nCk⋅3k (b) n+1Ck⋅3k (c) n+1Ck⋅3k−1 (d) nCk−1⋅3k
View SolutionIf n is a positive integer and Ck=nCk, then the value of n∑k=1k3(CkCk−1)2 is :
View Solution