A circle S of radius 'a' is the director circle of another circle S1,S1 is the director circle of circle S2 and so on. If the sum of the radii of all these circle is 2, then the value of 'a' is 2+√2 (b) 2−1√2 2−√2 (d) 2+1√2
Step by step video & image solution for A circle S of radius ' a ' is the director circle of another circle S_1,S_1 is the director circle of circle S_2 and so on. If the sum of the radii of all these circle is 2, then the value of ' a ' is 2+sqrt(2) (b) 2-1/(sqrt(2)) 2-sqrt(2) (d) 2+1/(sqrt(2)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A circle x2+y2+4x−2√2y+c=0 is the director circle of circle S1andS2, is the director circle of circle S1, and so on. If the sum of radii of all these circles is 2, then find the value of c.
View SolutionA circle x2+y2+4x−2√2y+c=0 is the director circle of the circle S1andS1 is the director circle of circle S2, and so on. If the sum of radii of all these circles is 2, then the value of c is k√2 , where the value of k is___________
View Solution
Knowledge Check
Three circles of radius 1 cm are circumscribed by a circle of radius r, as shown in the figure. Find the value of r?
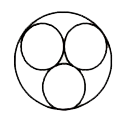
(a)√3+1
(b)2+√3√3
(c)√3+2√2
(d)2+√3A√3+1B2+√3√3C√3+2√2D2+√3
a circles S of radius 'a' is the director circle of another circle S1.S2 is the director circle of S2 and so on. If the sum of radius of S,S1,S2,S3…. circles is '2' and a=(k−√k), then the value of k is ……
View SolutionThe radius of the circle passing through the points (1,2),(5,2)and(5,−2) is : (A) 5√2 (B) 2√5 (C) 3√2 (D) 2√2
View SolutionIf C1:x2+y2=(3+2√2)2 is a circle and PA and PB are a pair of tangents on C1, where P is any point on the director circle of C1, then the radius of the smallest circle which touches c1 externally and also the two tangents PA and PB is 2√3−3 (b) 2√2−1 2√2−1 (d) 1
View SolutionThe equation of director circle to the circle x2+y2=8 is
View SolutionFind the equation of the circle with : Centre(−a,−b)andradius√a2−b2.
View SolutionIf m(x−2)+√1−m2y=3 , is tangent to a circle for all m∈[−1,1] then the radius of the circle is
View SolutionFind the equation of the circle with : Centre(1,1)andradius√2.
View Solution
