If A,B,C are three real numbers and p=[A+b+C] and q=[A]+[B]+[C]. (where [.] represents greatest integer function). Then maximum value of p−q is: 1 (b) 0 (c) 2 (d) 3
Step by step video & image solution for If A , B , C are three real numbers and p=[A+b+C] and q=[A]+[B]+[C]dot (where [.] represents greatest integer function). Then maximum value of p-q is: 1 (b) 0 (c) 2 (d) 3 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If a, b, c are positive real numbers such that a+b+c=1, then the greatest value of (1-a)(1-b)(1-c), is
A127B827C427D9If P=(a,b,c)andQ=(1,2), then the total number of relations P to Q are not functions is
A56B8C9D55
If a,b,c are positive real numbers such that a + b +c=18, find the maximum value of a2b3c4
View SolutionSECTION MULTIPLE CORRECT CHOICE TYPE Example 41 Let a, b, c , p, q be five different non-zero real numbers and x, y, z be three numbers satisfying the system of equations a a-p aq then (a) x + y + z = a + b + c-p-q abc (b) x = pq 0 in (c) y = (a-p)(h-p)(c-p) p(p-q) (a-q)(b-q)(c-q) aq-p) (d) z = b.
View SolutionMatch the following lists (where [x] represents the greatest integer function) and then choose the correct code.
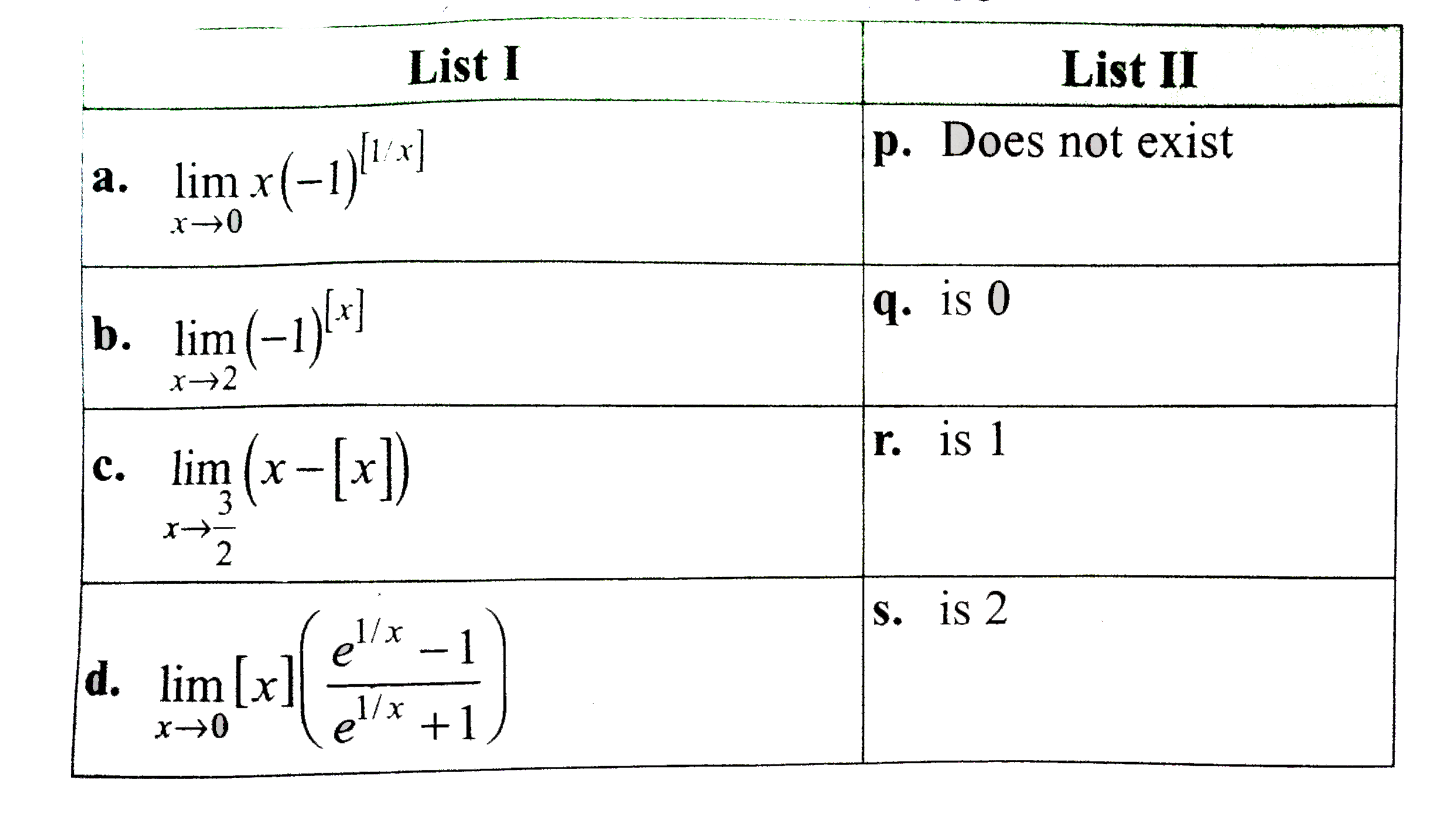
Codes :
a b c d(1)s r q p(2)q p s p(3)s r p q(4)p p q r
View SolutionIf a,b,c are three distinct positive real numbers in G.P., then prove that c2+2ab>3a⋅
View SolutionThe function 'f' is defined by f(x)=xp(1−x)q for all x ∈R, where p, q are positive integers, has a maximum value, for x equal to : pqp+q (b) 1 (c) 0 (d) pp+q
View SolutionIf three positive real numbers a,,b,c are in A.P. sich that abc=4 , then the minimum value of b is a.21/3 b. 22/3 c. 21/2 d. 23/23
View Solution
