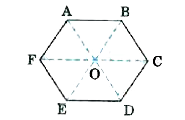
For a regular hexagon ABCDEF shown below , prove that
$- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F = 6 - - \to A O .$

Video Solution

Text Solution

Verified by Experts

Using triangle law of vector addition , we have
$- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F$
$= - - \to A B + (- - \to A D + - - \to D C) + - - \to A D + (- - \to A D + - - \to D E) + - - \to A F$
$= 3 - - \to A D + - - \to A B + - - \to D C + - - \to D E + - - \to A F$
$= 3 - - \to A D + (- - \to A B + - - \to D E) + (- - \to D C + - - \to A F) ⎛ ⎝ \begin{matrix} ∴ - - \to A B = - - - \to D E - - \to D C = - - - \to A F \end{matrix} ⎞ ⎠$
$= 3 (2 - - \to A O) + \to O + \to O$
$= 6 (- - \to A O)$
Hence proved

Updated on:21/07/2023

Let $\to C = \to A + \to B$ then :
A $∣ ∣ \to C ∣ ∣$ is always greater then $∣ ∣ \to A ∣ ∣$ and $∣ ∣ \to C ∣ ∣ < ∣ ∣ \to B ∣ ∣$
Bit is possible to have
C $∣ ∣ \to C ∣ ∣$ is always equal to $∣ ∣ \to A + \to B ∣ ∣$
D $∣ ∣ \to C ∣ ∣$ is never equal to $∣ ∣ \to A + \to B ∣ ∣$
The angle between vector $(\to A - \to B)$ and $(\to B \times \to A)$ is :
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
D $45^{\circ}$
what is the angle between $(\to P + \to Q)$ and $(\to P + \to Q)$ ?
A0
B $\frac{π}{2}$
C $\frac{π}{2}$
D $π$