A boy stands 19.6 m away from a 9.8m high cliff. If the throws a ball towards the cliff such that it just passes above from it , find the velocity of projection of the ball.
To solve the problem of finding the velocity of projection of the ball thrown by the boy towards the cliff, we can break down the solution step by step.
Step 1: Understand the Problem
The boy is standing 19.6 m away from a cliff that is 9.8 m high. He throws a ball such that it just passes above the cliff. We need to find the initial velocity of the ball when thrown at an angle.
Step 2: Identify the Maximum Height
Since the ball just passes above the cliff, the maximum height (h) that the ball reaches is equal to the height of the cliff, which is 9.8 m.
Step 3: Use the Maximum Height Formula
The formula for maximum height (h) in projectile motion is given by:
h=u2sin2θ2g
where:
- u = initial velocity of projection
- θ = angle of projection
- g = acceleration due to gravity (approximately 9.8m/s2)
Step 4: Use the Range Formula
The horizontal distance (range) covered by the projectile is given by:
R=u2sin2θg
where:
- R = horizontal distance (19.6 m in this case)
Step 5: Set Up the Equations
From the maximum height equation:
9.8=u2sin2θ2×9.8
This simplifies to:
u2sin2θ=9.8×19.6
u2sin2θ=192.08(1)
From the range equation:
19.6=u2sin2θ9.8
This simplifies to:
u2sin2θ=19.6×9.8
u2sin2θ=192.08(2)
Step 6: Relate sin2θ to sin2θ
Using the identity sin2θ=2sinθcosθ, we can express equation (2) as:
u2(2sinθcosθ)=192.08
Step 7: Solve for u
From equation (1):
u2sin2θ=192.08
From equation (2):
u2(2sinθcosθ)=192.08
Dividing the second equation by the first equation gives:
2sinθcosθsin2θ=1
This simplifies to:
2cosθ=sinθ
Thus, tanθ=2.
Step 8: Find θ
Using tanθ=2, we can find θ using the inverse tangent function:
θ=tan−1(2)
Step 9: Substitute Back to Find u
Now we can substitute back to find u. We can use either equation (1) or (2). Let's use equation (1):
u2=192.08sin2θ
We can find sin2θ using tanθ:
sin2θ=45(since sin2θ+cos2θ=1)
Thus:
u2=192.0845=240.1
Taking the square root gives:
u≈15.5m/s
Final Answer
The initial velocity of projection of the ball is approximately 15.5m/s.
---
The boy is standing 19.6 m away from a cliff that is 9.8 m high. He throws a ball such that it just passes above the cliff. We need to find the initial velocity of the ball when thrown at an angle.
Since the ball just passes above the cliff, the maximum height (h) that the ball reaches is equal to the height of the cliff, which is 9.8 m.
The formula for maximum height (h) in projectile motion is given by:
h=u2sin2θ2g
where:
- u = initial velocity of projection
- θ = angle of projection
- g = acceleration due to gravity (approximately 9.8m/s2)
The horizontal distance (range) covered by the projectile is given by:
R=u2sin2θg
where:
- R = horizontal distance (19.6 m in this case)
From the maximum height equation:
9.8=u2sin2θ2×9.8
This simplifies to:
u2sin2θ=9.8×19.6
u2sin2θ=192.08(1)
19.6=u2sin2θ9.8
This simplifies to:
u2sin2θ=19.6×9.8
u2sin2θ=192.08(2)
Using the identity sin2θ=2sinθcosθ, we can express equation (2) as:
u2(2sinθcosθ)=192.08
From equation (1):
u2sin2θ=192.08
From equation (2):
u2(2sinθcosθ)=192.08
2sinθcosθsin2θ=1
This simplifies to:
2cosθ=sinθ
Thus, tanθ=2.
Using tanθ=2, we can find θ using the inverse tangent function:
θ=tan−1(2)
Now we can substitute back to find u. We can use either equation (1) or (2). Let's use equation (1):
u2=192.08sin2θ
We can find sin2θ using tanθ:
sin2θ=45(since sin2θ+cos2θ=1)
Thus:
u2=192.0845=240.1
Taking the square root gives:
u≈15.5m/s
The initial velocity of projection of the ball is approximately 15.5m/s.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (1)
8 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A boy stands at 39.2 m from a building and throws a ball which just passes through a window 19.6 m above the ground. Calculate the velocity of projection of the ball.
View SolutionA body stans at 78.4m from a building and throws a ball which just enters a window 39.2m above the ground. Calculate the velocity of projection of the ball. Fig. 2 (d) . 22.
 .
.
View Solution
Knowledge Check
Two rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
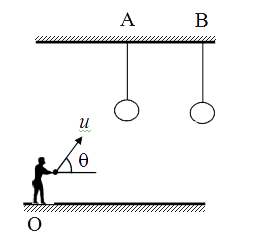
The angle of projection of the ball is:Atan−134Btan−143Ctan−112Dtan−135Two rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
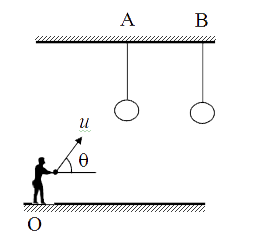
The projection speed of the ball is:A3 m/sB4 m/sC5 m/sD2.5 m/sA ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
Aα=tan−1(13)Bα=tan−1(2)Cα=tan−1(23)Dα=tan−1(24)
A man fires a shot and hears an echo from a cliff after 2s. He walks 85m towards the cliff and the echo of a second shot is now heard after 1.4s. What is the velocity of sound and how far was the man from the cliff when he first heard the echo ?
View SolutionA man fires a shot and hears an echo from a cliff after 2s. He walks 85m towards the cliff and the echo of a second shot is now heard after 1.4s. What is the velocity of sound and how far was the man from the cliff when he first heard the echo ?
View SolutionA boat is rowed away from a cliff 150 m high. At the top of the cliff, the angle of depression of the boat changes from 60° to 45° in 2.5 minutes. The speed of the boat (in m/sec) is
View SolutionA ball was thrown by a boy a at angle 60∘ with horizontal at height 1 m from ground. Boy B is running in the plane of motion of ball and catches the ball at height 1 m from ground. He finds the ball falling vertically. If the boy is running at a speed 20 km/hr. Then the velocity of projection of ball is-
View SolutionA shell is fired with a horizontal velocity in the positive x direction from the top of an 80 m high cliff. The shell strikes the ground 1330 m from the base of the cliff. The drawing is not to scale.
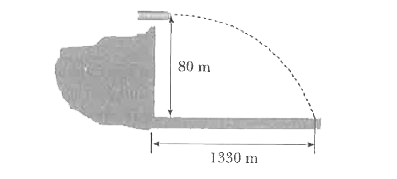
What is the magnitude of the acceleration of the shell just before is strikes the ground?
View Solution
