Question

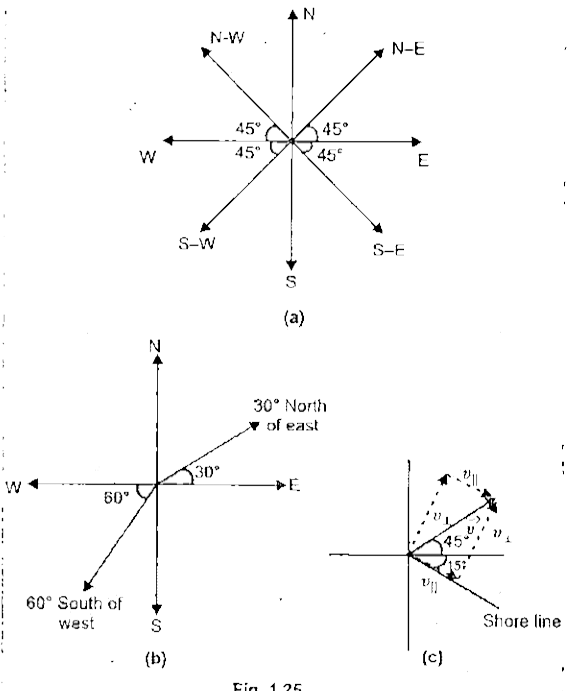
A man rides a jet boat with a speed of $40km/hr$ in the north -east direction and the shore line makes an angle of ${10}^{\circ }$ south of east . Find the component of the velocity of the jet boat
(i) along the shoreline and
(ii) perpendicular to the shoreline .

Explanation

To solve the problem, we need to find the components of the velocity of the jet boat in two directions: along the shoreline and perpendicular to the shoreline.

1. Identify the Given Information:
- Speed of the jet boat, \( v = 40 \, \text{km/hr} \)
- Direction of the jet boat: North-East (which is at an angle of \( 45^\circ \) from the East).
- The angle of the shoreline with respect to the East: \( 10^\circ \) South of East.

2. Determine the Total Angle:
- The angle between the direction of the jet boat and the shoreline can be calculated. The jet boat is at \( 45^\circ \) (North-East) and the shoreline is at \( 10^\circ \) (South of East).
- Therefore, the angle between the jet boat's direction and the shoreline is:
\( \text{Total angle} = 45^\circ + 10^\circ = 55^\circ \)

3. Calculate the Component of Velocity Along the Shoreline:
- The component of the velocity along the shoreline can be found using the cosine of the angle:
\( v_{\text{along}} = v \cdot \cos(\text{Total angle}) = 40 \cdot \cos(55^\circ) \)
- Using a calculator, we find:
\( \cos(55^\circ) \approx 0.5736 \)
- Therefore:
\( v_{\text{along}} = 40 \cdot 0.5736 \approx 22.94 \, \text{km/hr} \)

4. Calculate the Component of Velocity Perpendicular to the Shoreline:
- The component of the velocity perpendicular to the shoreline can be found using the sine of the angle:
\( v_{\text{perpendicular}} = v \cdot \sin(\text{Total angle}) = 40 \cdot \sin(55^\circ) \)
- Using a calculator, we find:
\( \sin(55^\circ) \approx 0.8192 \)
- Therefore:
\( v_{\text{perpendicular}} = 40 \cdot 0.8192 \approx 32.77 \, \text{km/hr} \)

Final Answers:
(i) The component of the velocity of the jet boat along the shoreline is approximately 22.94 km/hr.
(ii) The component of the velocity of the jet boat perpendicular to the shoreline is approximately 32.77 km/hr.