A thin metallic wire is bent into a shape as shown in figure.

O is the common centre of all the circular arcs. What is the magnetic field at O?
Magnetic field at point O due to straight conductors OF, ED and CB will be zero.
Magnetic field due to circular are subtending angle θ at the centre can be written as:
B=θ2πμ0I2r=θμ0I4πr
Magnetic field at point O due to circular are EF of radius r1=0.01m can be calculated as:
B1=μ0I4πr×π6
[∴ Radian measure of 30∘ is π6]
=μ04π×5(0.01)×π6=10−7×50.01×227×6
=2.62×10−5T (outwards)
Magnetic field at point O due to circular are CD of radius r2=0.02 n can be calculated as :
B2=μ0I4πr2×π6
=μ04π×5(0.02)×π6=10−7×50.02×227×6
=1.31×10−5 T ( inwards)
Magnetic field at point O due to circular are AB of radius r3=0.03 m can be calculated as :
B3=μ0I4πr2×π6
=μ04π5(0.08)×π6=10−7×50.03×227×6
=8.7×10−6 T (outwards)
Net magnetic field at point O can be calculated as :
B=B1−B2+B3
=[2.62−1.31+0.87]×10−5T
=2.18×10−5T (outwards)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - PRACTICE PROBLEMS
59 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions
29 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
An infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
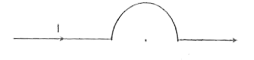
View SolutionA current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
View Solution
Knowledge Check
A current carrying wire is bent in the L shapes as shown in figure. The length of both arms extend to infinity. Then, the magnetic field at O is-
 AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)
AzeroBμ0I/2πrCμ0I2πr(1+1√2)Dμ0I4πr(1+1√2)The magnetic field at the centre O of the are shown in the figure is
 A2I(√2+π)×10−7rB2I(√2+π4)×10−7rCI(√2+π)×10−7rDI(√2+π4)×10−7r
A2I(√2+π)×10−7rB2I(√2+π4)×10−7rCI(√2+π)×10−7rDI(√2+π4)×10−7rA long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is
 A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
B0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png)
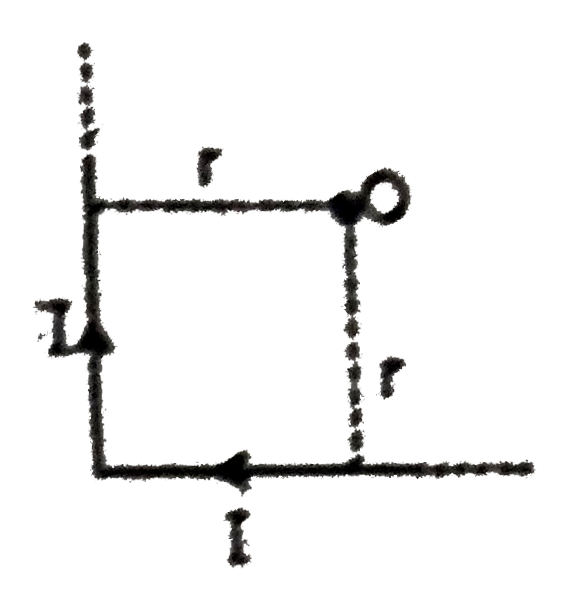
View SolutionThe current loop abcde formed by two circular segments of radii r1(=4cm) and r2(=6cm) with common centre at O, carries a current I(=2A) as shown in figure. What is the magnetic field at the common centre O? What will be the value of magnetic field at O when θ=90∘?
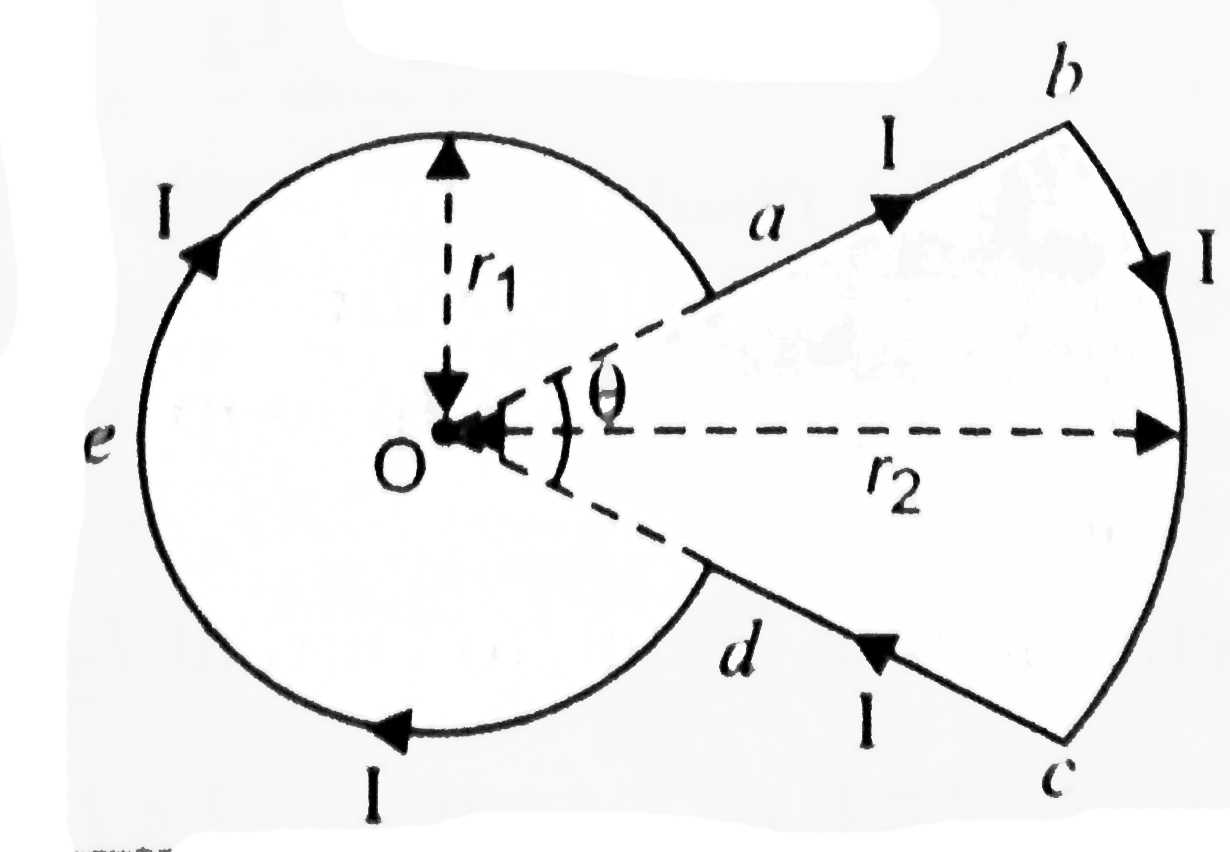
View SolutionThe magnetic field at the centre O of the are shown in the figure is
View SolutionA straight wire carrying a current of 12A is bent into a semicircular arc of radius 2⋅0cm as shown in figure. Consider the magnetic field →B at the centre of arc.
(a) What is the magnetic field due to the staight segments?
(b) In what way the contribution to →B from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semicircle arc of the same radius but in the opposite way as shown in figure

View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View Solution
