A current carrying wire A is carrying current of 10 A from east to west and is fixed. Another wire B of maas 5 g, length 2 m and carrying a current 20 A is placed below the wire such that it remains suspended due to the magnetic force. Find the position of wire B and also indicate the direction of current in B. Take g=10m/s2.
To solve the problem, we need to analyze the forces acting on wire B due to the magnetic field created by wire A, and then find the position of wire B such that it remains suspended.
1. Identify the Forces Acting on Wire B:
- Wire B has a mass m=5g=0.005kg.
- The weight of wire B is given by W=m⋅g=0.005kg⋅10m/s2=0.05N.
- For wire B to remain suspended, the magnetic force acting on it must equal its weight: FB=W.
2. Determine the Magnetic Field due to Wire A:
- Wire A carries a current IA=10A from east to west.
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- Here, μ0=4π×10−7T m/A.
3. Calculate the Magnetic Force on Wire B:
- Wire B carries a current IB=20A and has a length L=2m.
- The magnetic force FB on wire B due to the magnetic field B is given by:
FB=IB⋅L⋅B
4. Set the Forces Equal:
- For wire B to be suspended:
FB=W⟹IB⋅L⋅B=W
- Substituting the values:
20⋅2⋅B=0.05
- Simplifying gives:
40B=0.05⟹B=0.0540=0.00125T
5. Find the Distance r:
- Using the expression for B:
0.00125=4π×10−7⋅102πr
- Simplifying gives:
0.00125=2×10−6r⟹r=2×10−60.00125=1.6m
6. Determine the Direction of Current in Wire B:
- According to the right-hand rule, if the current in wire A flows from east to west, the magnetic field circles around wire A.
- For wire B to experience an upward force (to counteract its weight), the current in wire B must flow from west to east.
Final Answers:
- The position of wire B is 1.6 m below wire A.
- The direction of current in wire B is from west to east.
- Wire B has a mass m=5g=0.005kg.
- The weight of wire B is given by W=m⋅g=0.005kg⋅10m/s2=0.05N.
- For wire B to remain suspended, the magnetic force acting on it must equal its weight: FB=W.
- Wire A carries a current IA=10A from east to west.
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- Here, μ0=4π×10−7T m/A.
- Wire B carries a current IB=20A and has a length L=2m.
- The magnetic force FB on wire B due to the magnetic field B is given by:
FB=IB⋅L⋅B
- For wire B to be suspended:
FB=W⟹IB⋅L⋅B=W
- Substituting the values:
20⋅2⋅B=0.05
- Simplifying gives:
40B=0.05⟹B=0.0540=0.00125T
- Using the expression for B:
0.00125=4π×10−7⋅102πr
- Simplifying gives:
0.00125=2×10−6r⟹r=2×10−60.00125=1.6m
- According to the right-hand rule, if the current in wire A flows from east to west, the magnetic field circles around wire A.
- For wire B to experience an upward force (to counteract its weight), the current in wire B must flow from west to east.
- The position of wire B is 1.6 m below wire A.
- The direction of current in wire B is from west to east.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - PRACTICE PROBLEMS
59 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions
29 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
Knowledge Check
A current carrying power line carries current from west to east. The direction of magnetic field 1m above is
Anorth to southBsouth to northCeast to westDwest to eastA long straight wire is carrying a current of 25 A. A square loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is
 A3.1×10−3N towards the wireB3.1×10−4N towards from the wireC9.4×10−4N towards the wireD9.4×10−4N away from the wire.
A3.1×10−3N towards the wireB3.1×10−4N towards from the wireC9.4×10−4N towards the wireD9.4×10−4N away from the wire.Two parallel wires carry currents of 10A and 40A in opposite directions.Another wire carrying a current antiparallel to 10A is placed midway between the two wires.The magnetic force on it will be
Atowards 20ABtowards 40ACzeroDperpendicular to the plane of the currents
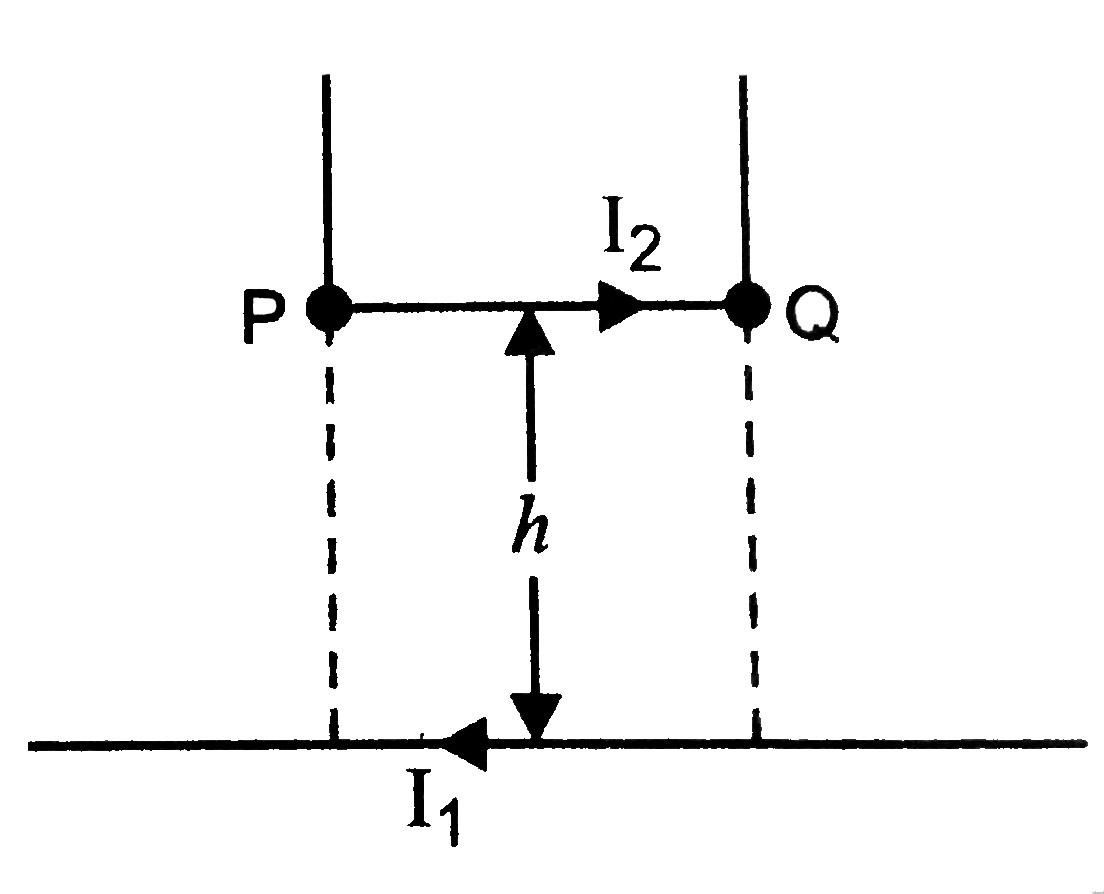
A long straight wire carrying current of 25A rests on a table as shown in figure. Another wire PQ of length 1m, mass 2⋅5g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?
View SolutionTwo parallel wires carry currents of 20A and 40A in opposite directions. Another wire carrying a current antiparallel to 20A is placed midway between the two wires. The magnetic force on it will be
View SolutionA wire AB is carrying current of 12 A and is lying on the table. Another wire CD carrying 5 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB . [Take the value of g=10ms−2]
View SolutionTwo parallel wires carry currents of 20A and 40A in same direction. Another wire carrying a current anti- parallel to 20A is placed midway between the two wires. The magnetic force on it will be
View SolutionA straight wire of diameter 0.4 mm carrying a current of 2A is replaced by another wire of 0.8 mm diameter and carrying the same current. The magnetic field at the same distance from the wire is
View Solution
