An iron rod of mass 50 g and length 50 cm is suspended by master wires as shown in the figure. Calculate the magnitude and direction of magnetic field to be set in the region such that the tension is the wires is zero. The current in the rod is 4 A.

The correct Answer is:0.25T
Step by step video, text & image solution for An iron rod of mass 50 g and length 50 cm is suspended by master wires as shown in the figure. Calculate the magnitude and direction of magnetic field to be set in the region such that the tension is the wires is zero. The current in the rod is 4 A. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions29videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Tough & Tricky (PROBLEMS )15videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST13videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
Two long thin wires ABC and DEF are arranged as shown in the figure. They carry currents I. The magnitude of the magnetic field at O is
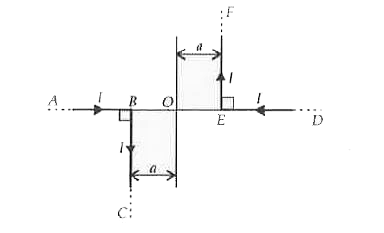 AzeroBμ0I4πaCμ0I2πaDμ0I√2πa
AzeroBμ0I4πaCμ0I2πaDμ0I√2πa - Question 2 - Select One
A straight horizontal conducting rod of length 50 cm and mass 50 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (take=10ms−2
A0.05TB0.1TC0.2TD0.5T - Question 3 - Select One
A straight horizontal conducting rod of length 50 cm and mass 50 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero? (Take g=10 m s−2)
A0.05 TB0.1 TC0.2 TD0.5 T
A current of I ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field at O is
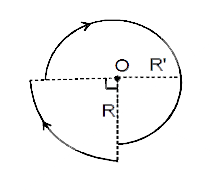 View Solution
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
 View Solution
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionA straight horizontal conducting rod of length l and mass m is suspended by two vertical wires at its ends. A current I is set up in the rod through the wires.
(i) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero.
(ii) What will be the total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before?View SolutionThe wire shown in the figure, carries a current of 60A. Determine the magnitude of the magnetic field induction at O. Given radius of the bent coil is 2cm.
 View Solution
View Solution