A wire is bent forming two semicircles as shown in the figure. Calculate the magnitude of magnetic intensity at the centre.

The correct Answer is:μ0I4(b=aab)
Step by step video, text & image solution for A wire is bent forming two semicircles as shown in the figure. Calculate the magnitude of magnetic intensity at the centre. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions29videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Tough & Tricky (PROBLEMS )15videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST13videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
An equilateral triangle of side length l is formed from a piece of wire of uniform resistance. The current I is as shown in figure. Find the magnitude of the magnetic field at its centre O.
 View Solution
View SolutionA uniform wire of length l and mass M is bent in the shape of a semicircle of radius r as shown in figure. Calculate moment of intertia about the axis XX'
View Solution
Knowledge Check
- Question 1 - Select One
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
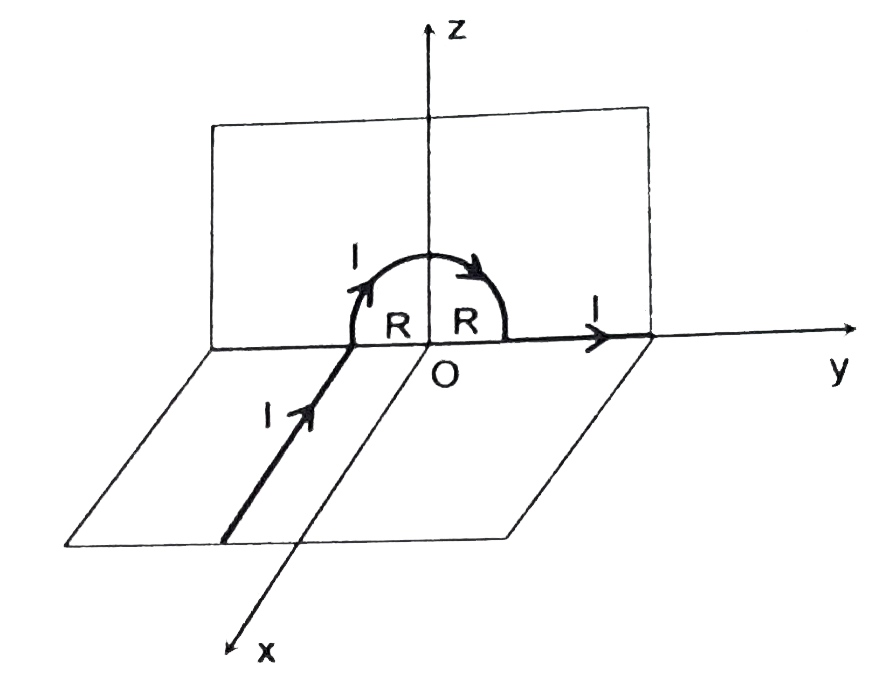 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2 - Question 2 - Select One
A conductor is bent in the form of concentric semicircles as shown in the figure. The magnetic field at the point o
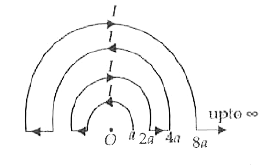 AzeroBμ0I6aCμ0IaDμ0I4a
AzeroBμ0I6aCμ0IaDμ0I4a - Question 3 - Select One
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
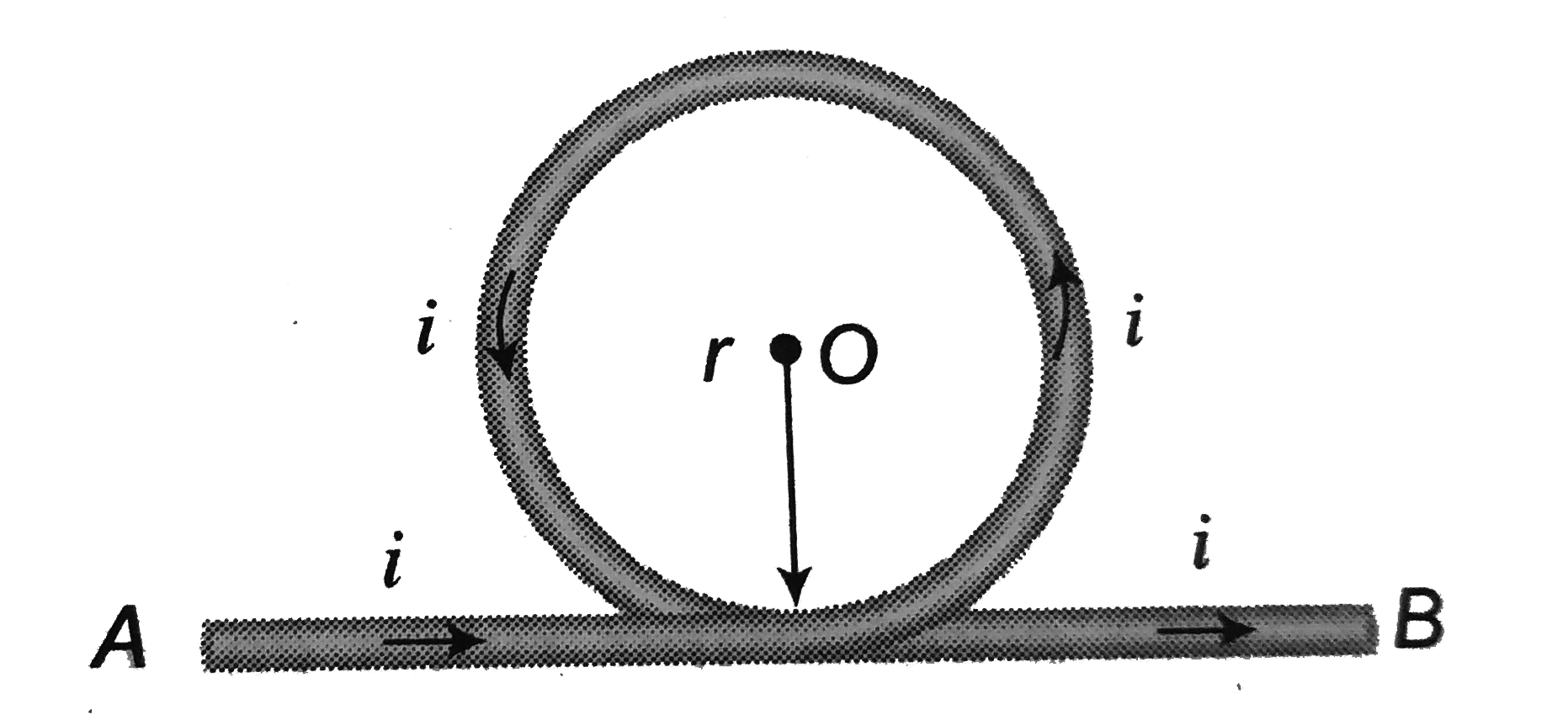 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
A straight conducting wire is bent as shown in the adjoining figure. Calculate the magnetic field at point O.
 View Solution
View SolutionTwo wires A and B have the same length equal to 44cm. and carry a current of 10A each. Wire A is bent into a circle and wire B is bent into a square. (a) Obtain the magnitudes of the fields at the centres of the two wires. (b) Which wire produces a greater magnetic field at the centre?
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionA straight wire carrying a current of 12A is bent into a semicircular arc of radius 2⋅0cm as shown in figure. Consider the magnetic field →B at the centre of arc.
(a) What is the magnetic field due to the staight segments?
(b) In what way the contribution to →B from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semicircle arc of the same radius but in the opposite way as shown in figure
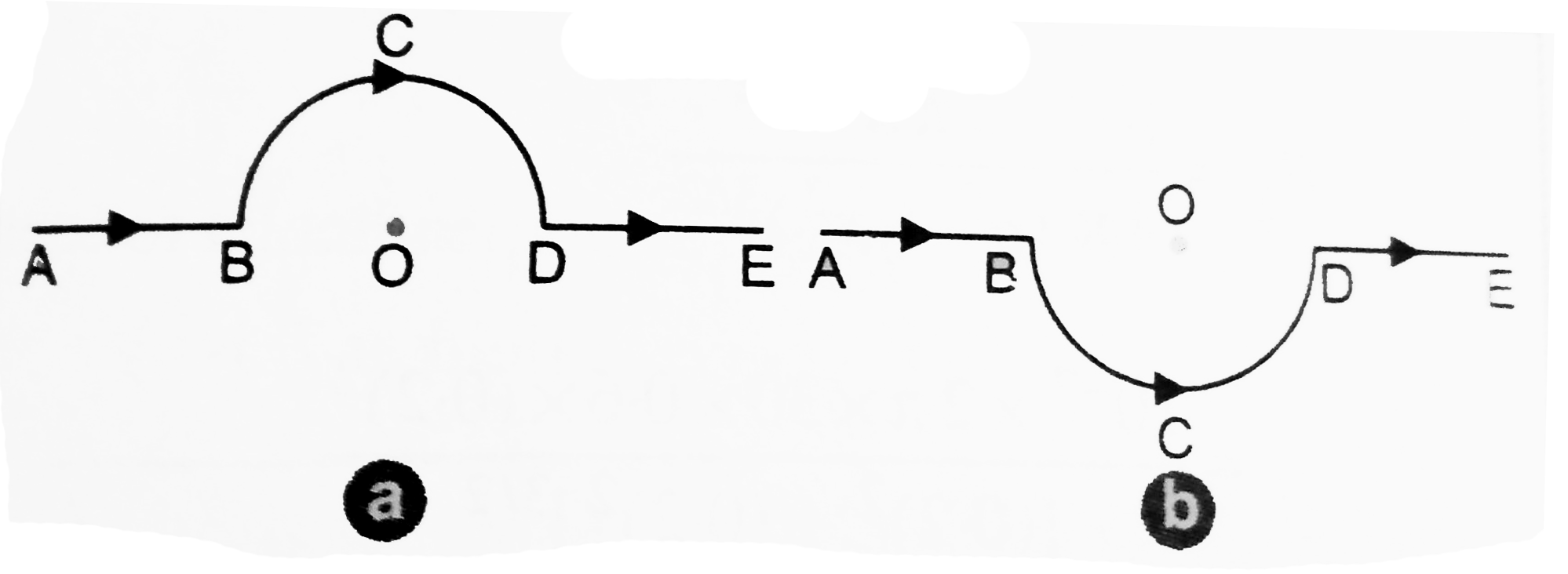 View Solution
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View Solution

