A copper wire of length 7 metre is bent to form a circular loop. If i current flows through the loop, find out the magnitude of magnetic moment of the loop.
To find the magnitude of the magnetic moment of a circular loop formed by bending a copper wire of length 7 meters, we can follow these steps:
Step 1: Determine the radius of the circular loop
The length of the wire is equal to the circumference of the circular loop. The formula for the circumference C of a circle is given by:
C=2πR
where R is the radius of the circle. Given that the length of the wire is 7 meters, we can set up the equation:
2πR=7
To find R, we rearrange the equation:
R=72π
Step 2: Calculate the area of the circular loop
The area A of a circle is given by the formula:
A=πR2
Substituting the expression for R from Step 1:
A=π(72π)2
Calculating this, we have:
A=π⋅494π2=494π
Step 3: Use the formula for magnetic moment
The magnetic moment M of a current-carrying loop is given by the formula:
M=I×A
where I is the current flowing through the loop. Substituting the area A from Step 2:
M=I×494π
Final Expression
Thus, the magnitude of the magnetic moment of the loop is:
M=49I4π
Summary
The final answer for the magnitude of the magnetic moment of the loop is:
M=49I4π
The length of the wire is equal to the circumference of the circular loop. The formula for the circumference C of a circle is given by:
C=2πR
where R is the radius of the circle. Given that the length of the wire is 7 meters, we can set up the equation:
2πR=7
To find R, we rearrange the equation:
R=72π
The area A of a circle is given by the formula:
A=πR2
Substituting the expression for R from Step 1:
A=π(72π)2
Calculating this, we have:
A=π⋅494π2=494π
The magnetic moment M of a current-carrying loop is given by the formula:
M=I×A
where I is the current flowing through the loop. Substituting the area A from Step 2:
M=I×494π
Thus, the magnitude of the magnetic moment of the loop is:
M=49I4π
The final answer for the magnitude of the magnetic moment of the loop is:
M=49I4π
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Additional Questions )
16 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Fill in the Blanks )
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Higher Order Thinking Skills & Advanced Level
10 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Draw the magnetic field lines due to a circular current loop placed in a horizontal plane.
An enamelled copper wire of length L is bent in the form of a circular loop and a curretn I is passed through it so that a magnetic field B is get up at its centre. Now the same wire is bent in the form of a circular coil having N turns and same current I is passed through it. What is the magnetic field develop at the centre of this coil?
View SolutionTwo identical wires each of length L are bent to form a circular loop and a square loop. If the same current i flows in the two wires, then the ratio of the magnetic inductions at the centre of the circular and square loops is :
View Solution
Knowledge Check
The magnitude of magnetic moment of the current loop in the figure is
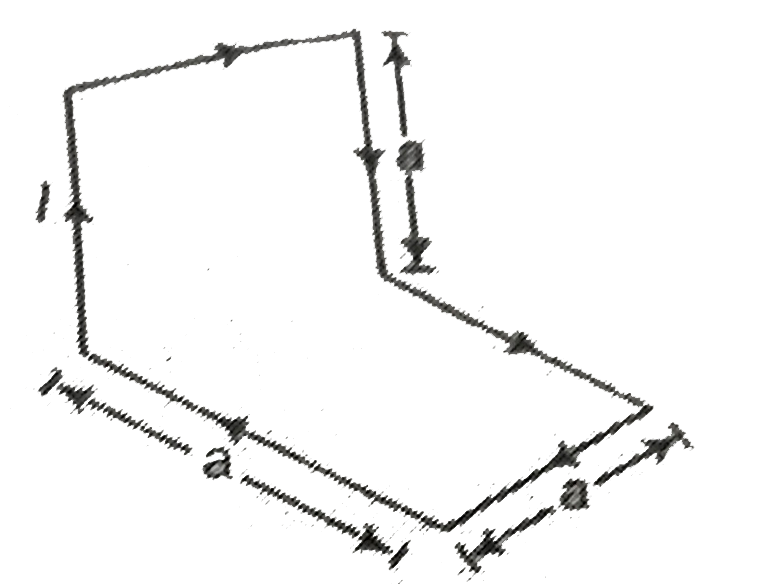 Ala2B√2la2CzeroDnone of the above
Ala2B√2la2CzeroDnone of the aboveA square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this square loop is changed to a circular loop and it carries the current, the magnitude of the magnetic dipole moment of circular loop will be :
A4mπB2mπC3mπDmπOn meter length of wires carriers a constant current. The wire is bent to from a circular loop. The magnetic field at the centre of this loop is B. The same is now bent to form a circular loop of smaller radius to have four turns in the loop. The magnetic field at the centre of this loop B. The same is now bent to form a circular loop of smaller radius of have four turns in the loop. The magnetic field at the centre of this new loop is
A4BB16BCB/2DB/4
A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m.If this square loop is changed to a circular loop and it carries the same current the magnitude of the magnetic dipole moment of circular loop will be
View SolutionThe magnitude off magnetic moment of the current loop in the figure is

View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View SolutionEqual current I flows in two segments of a circular loop in the direction shown in figure. Radius of the loop is 7. The magnitude of magnetic field induction at the centre of the loop O is
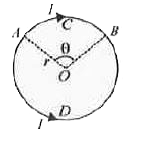
View SolutionA wire of length l carries a steady current. It is bent first to form a circular plane loop of one turn. The magnetic field at the centre of the loop is B. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same is
View Solution
