The lengths of three line segments (in cm) are given in each of the four cases. Which one of the the following cases is not suitable to be the three sides of a triangle?
The correct Answer is:B
To determine which set of line segments cannot form a triangle, we will apply the triangle inequality theorem. According to this theorem, for any three sides a, b, and c of a triangle, the following conditions must hold:
1. a+b>c
2. a+c>b
3. b+c>a
We will check each of the four cases provided.
Case 1: Sides = 2, 3, 4
1. Check 2+3>4:
- 5>4 (True)
2. Check 2+4>3:
- 6>3 (True)
3. Check 3+4>2:
- 7>2 (True)
All conditions are satisfied. Therefore, these sides can form a triangle.
Case 2: Sides = 2, 3, 5
1. Check 2+3>5:
- 5>5 (False)
2. Check 2+5>3:
- 7>3 (True)
3. Check 3+5>2:
- 8>2 (True)
Since the first condition is not satisfied, these sides cannot form a triangle.
Case 3: Sides = 2, 4, 5
1. Check 2+4>5:
- 6>5 (True)
2. Check 2+5>4:
- 7>4 (True)
3. Check 4+5>2:
- 9>2 (True)
All conditions are satisfied. Therefore, these sides can form a triangle.
Case 4: Sides = 3, 4, 5
1. Check 3+4>5:
- 7>5 (True)
2. Check 3+5>4:
- 8>4 (True)
3. Check 4+5>3:
- 9>3 (True)
All conditions are satisfied. Therefore, these sides can form a triangle.
Conclusion
The only case that does not satisfy the triangle inequality theorem is Case 2: Sides = 2, 3, 5. Thus, these sides cannot form a triangle.
---
2. a+c>b
3. b+c>a
- 5>4 (True)
2. Check 2+4>3:
- 6>3 (True)
3. Check 3+4>2:
- 7>2 (True)
- 5>5 (False)
2. Check 2+5>3:
- 7>3 (True)
3. Check 3+5>2:
- 8>2 (True)
- 6>5 (True)
2. Check 2+5>4:
- 7>4 (True)
3. Check 4+5>2:
- 9>2 (True)
- 7>5 (True)
2. Check 3+5>4:
- 8>4 (True)
3. Check 4+5>3:
- 9>3 (True)
The only case that does not satisfy the triangle inequality theorem is Case 2: Sides = 2, 3, 5. Thus, these sides cannot form a triangle.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Which one of the following cannot be represented by the three sides of a triangle?
A5,9,11B3,7,11C7,10,13D3,8,9 - Question 2 - Select One
The three sides of a triangles are given which one of the following is not a right angle :
A20,21,29B16,63,65C5690106D36,35,74 - Question 3 - Select One
The three sides of a triangles are given which one of the following is not a right angle :
A20, 21, 29B16, 63, 65C56, 90, 106D36,35, 74
Find magnetic moment in following cases
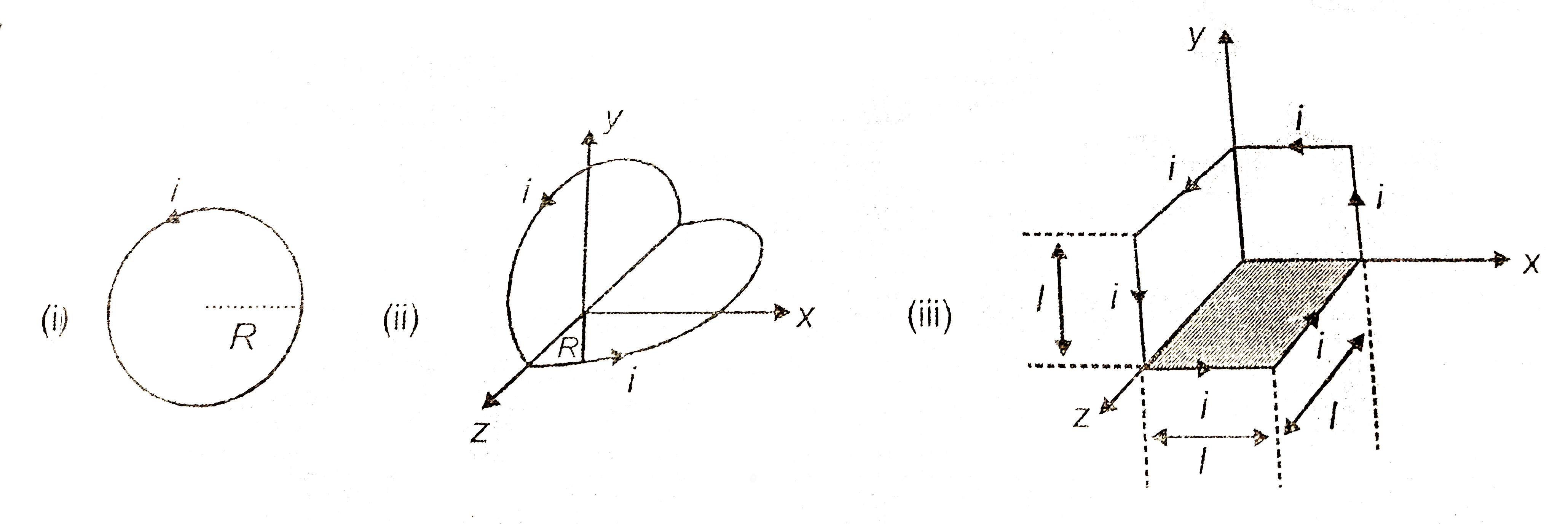
(Eash segment is of length l)View SolutionSides the three line segments ABBC and CA that form the triangle ABC are called the sides of the triangle ABC.
View SolutionThe lengths of two sides of a right angled triangle which contain the right angle are a and b respectively. Three squares are drawn on the three sides of the triangle on the outer side. What is the total area of the triangle and the three squares
View SolutionIn which one of the following cases, ΔHandΔU are not equal to each other?
View SolutionThe lengths of the sides of a Δ ABC are given below. In which of these cases are angles of the triangle in the increasing order of magnitude as ∠C,∠B,∠A.
View Solution

