Under suitable conditions two a-particles can combine to produce a proton and a nuclide of What minimum K.E. must the -particle have in order that the reaction, may proceed. The range of nuclear interaction is
2.2MeV
0.576MeV
1.6MeV
3.2MeV
The correct Answer is:B
Then, the - particle must have sufficient velocity to come within the range of nuclear interaction which is .
Topper's Solved these Questions
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - MCQ (Level -III)
9 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Recent Competitive Questions
31 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - RECENT COMPETITIVE QUESTIONS
32 Videos
Similar Questions
Assume that a particle cannot be confined to a sphereical volume of diameter less than De Broglie wavelength of the particle. Estimate the minimum kinetic energy a proton confined to a nucleus f diameter 10−14 m may have.
View SolutionA nuclear reaction is represented by the equation :
.21H+.21H→.32He+xc+E
(a) Name the process represented by this equation and describe what happens during this reaction.
(b) Identify the particle c and the number x of such particles produced in the reaction.
(c ) What does E represent ?
(d) State two conditions under which such a reaction takes place.
(e) What type of nuclear bomb is based on similar reactions ?
View Solution
Knowledge Check
A cyclotron is used to accelerate protons, deutrons, alpha-particles,etc. The maxumum kinetic energy acquired by the accelerated protons is E. What will be the maximum K,E, acquired by the alpha-partcles if they are accelarated under the same experimental conditions?
AEBE2C4ED2ERead the following passage carefully and answer the questions
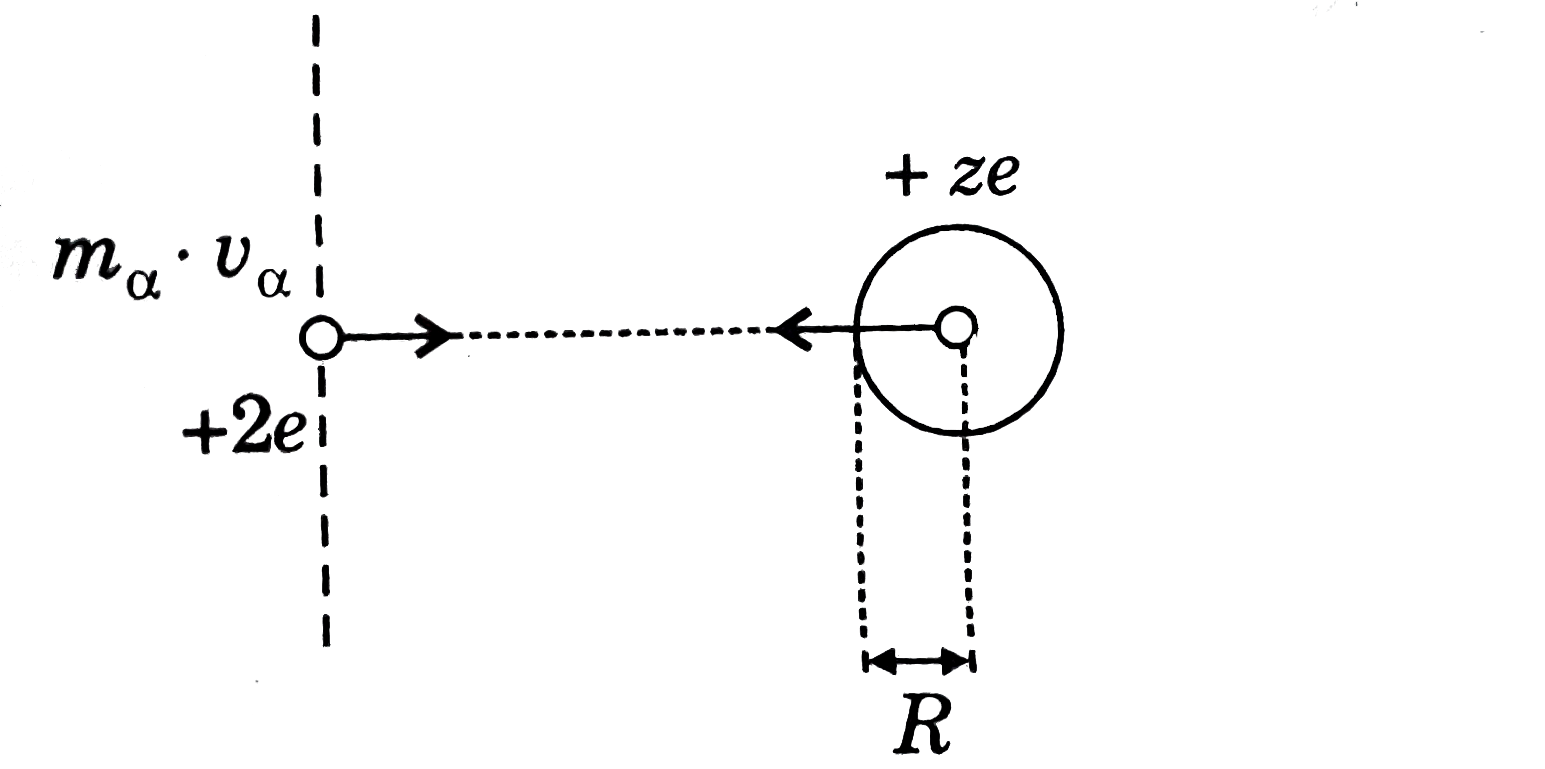
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of α−particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , α−particle with half of the earlier speed then the percentage error involved in the radius calculation is :A0.75B1C3D4An electron, a proton and an alpha particle have KE of 16E, 4E and E respectively. What is the qualitative order of their de-Broglie wavelengths?
Aλe>λp>λαBλp=λα>λeCλe>λp=λαDλα>λe>λp
An electron, a proton and an alpha particle have KE of 16E, 4E and E respectively. What is the qualitative order of their de-Broglie wavelengths?
View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:
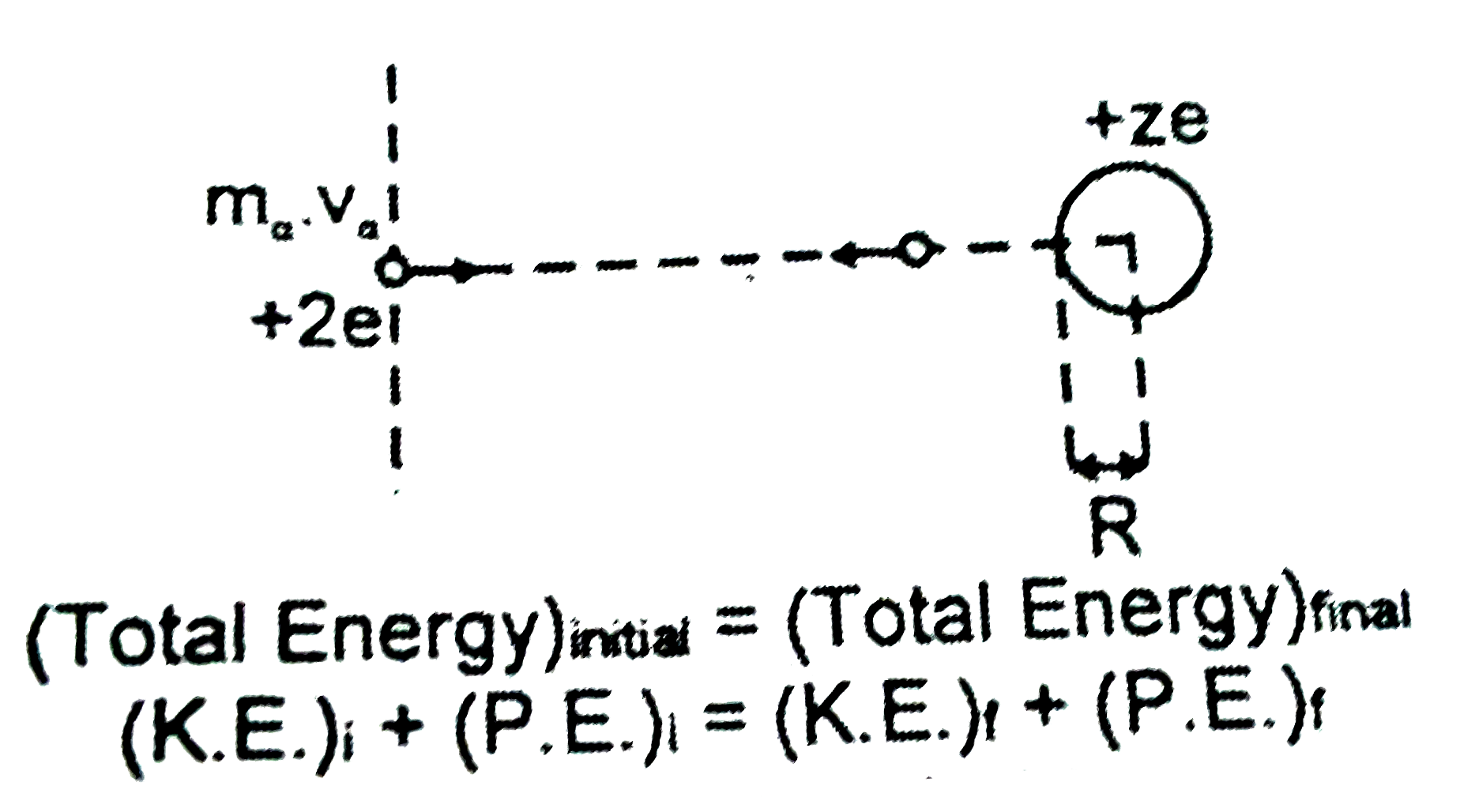
(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
Radius of a particular nucleus is calculated by the projection of α-particle from infinity at a particular speed. Let this radius is the true radius . If the radius calculation for the same nucleus is made by another α-particle with half of the earlier speed, then the percentage error involved in the radius calculation is :
View SolutionIn the disintegration of a radioactive element, α and β-particles are evolved from the nucleus:
.10n→.11H+.0−1e + Antineutrino + Energy
4.11H→.42He+2.0+1e + Energy
Then, emission of these particles changes the nuclear configuration and results into a daughter nuclide. Emission of an α-particles results into a daughter element having atomic number lowered by 2 and mass number by 4, on the order hand, emission of a β-particle yields an element having atomic number raised by one. soddy and Fajan proposed that the daughter nuclide may occupy different positions in the periodic talbe.
Select the correct statements amont the following:
View SolutionUnstable nuclei attain stability through disintegration. The nuclear stability is related to neutron proton ratio (n/p). For stable nuclei n/p ratio lies close to unity for elements with low atomic numbers (20 or less) but it is more than 1 for nuclei having higher atomic numbers. Nuclei having n/p ratio either very high or low undergo nuclear transformation. when n/p ratio is higher than required for stabilioty, the nuclei have the tendency to emit β-rays. While when n/p ratio is lower than required for stability, the nucleieither emits α-particles or a position or capture K-electron.
The order of radioactive disinigration is
View SolutionAn electron, a proton and an alpha particle have KE of 16E, 4E and E respectively. What is the qualitative order of their de-Broglie wavelengths?
View Solution
