A block of mass M is placed on a smooth table. Its two sides are attached to fixed walls by means of collinear horizontal springs of spring constants k1 and k2(k1>k2) as shown in the Figure. The block is made to oscillate horizontally along the line of the two springs.
The frequency of its oscillation is :
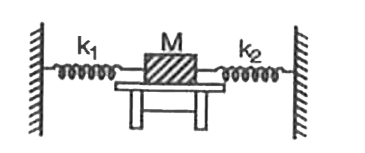
12π(k1+k2M)12
12π(k1−k2M)∧(12)
12π(Mk1+k2)12
12π(Mk1−k2)12.
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
A block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
A block of mass M is placed on a smooth table. Its two sides are attached to the fixed walls by means of collinear horizontal springs of spring constants K1 and K2 respectively (K1>K2) as shown in the figure. The block is made to oscillate horizontally along the line of two springs. The frequency of its oscillation is
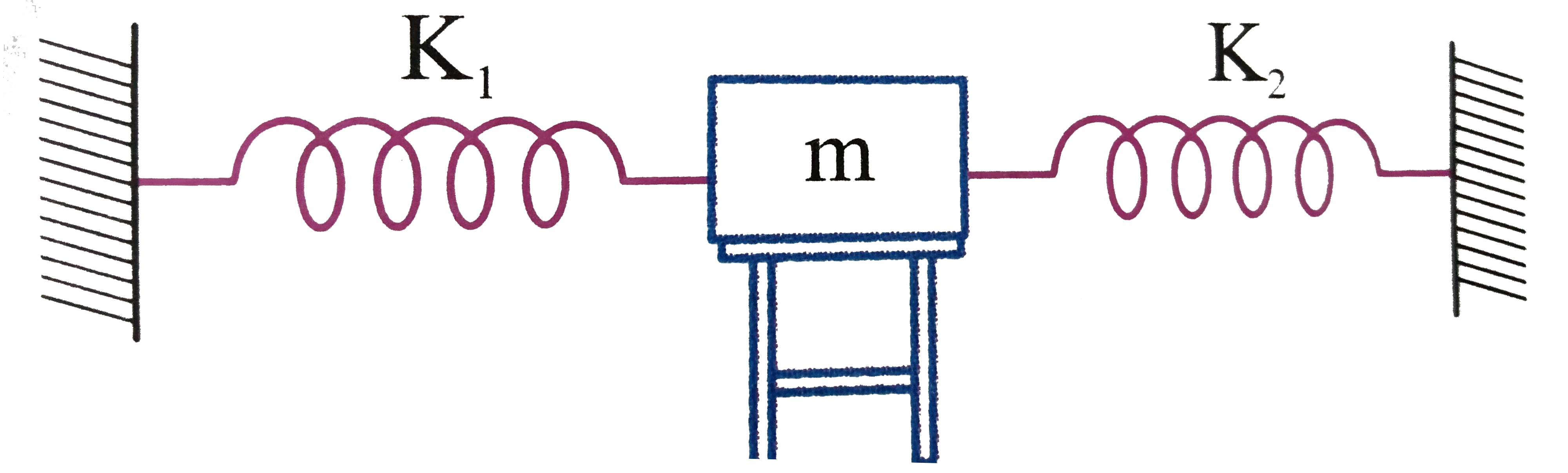 A12π ⎷(K1K2(K1+K2)M)B12π√(MK1+K2)C12π√(K1+K2M)D12π√(K1−K2M)
A12π ⎷(K1K2(K1+K2)M)B12π√(MK1+K2)C12π√(K1+K2M)D12π√(K1−K2M)A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
Two springs of force constants K1 and K2 are connected to a mass m as shown I the figure.

If both K1 and K2 are made four times their original values, the frequency of oscillation becomes,
View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View Solution
