(a) 1.20 (b) (c) (d)
To solve the problem 3.87¯¯¯¯¯¯87−2.59¯¯¯¯¯¯59, we will follow these steps:
Step 1: Understand the repeating decimals
The notation 3.87¯¯¯¯¯¯87 means that the digits "87" repeat indefinitely. Therefore, we can express it as:
3.87¯¯¯¯¯¯87=3+0.87¯¯¯¯¯¯87
Similarly, for 2.59¯¯¯¯¯¯59:
2.59¯¯¯¯¯¯59=2+0.59¯¯¯¯¯¯59
Step 2: Convert the repeating decimals to fractions
To convert 0.87¯¯¯¯¯¯87 into a fraction, we can set:
x=0.87¯¯¯¯¯¯87
Then, multiplying by 100 (to shift the decimal point two places to the right):
100x=87.87¯¯¯¯¯¯87
Now, subtracting the original x:
100x−x=87.87¯¯¯¯¯¯87−0.87¯¯¯¯¯¯87
This simplifies to:
99x=87
Thus:
x=8799=2933
So, we have:
0.87¯¯¯¯¯¯87=2933
For 0.59¯¯¯¯¯¯59:
Let:
y=0.59¯¯¯¯¯¯59
Then, multiplying by 100:
100y=59.59¯¯¯¯¯¯59
Subtracting the original y:
100y−y=59.59¯¯¯¯¯¯59−0.59¯¯¯¯¯¯59
This simplifies to:
99y=59
Thus:
y=5999
Step 3: Substitute back into the equation
Now substituting back into the original expression:
3.87¯¯¯¯¯¯87−2.59¯¯¯¯¯¯59=(3+2933)−(2+5999)
This simplifies to:
(3−2)+(2933−5999)
Calculating 2933−5999:
To subtract these fractions, we need a common denominator. The least common multiple of 33 and 99 is 99. Thus, we convert 2933:
2933=29×333×3=8799
Now we can perform the subtraction:
8799−5999=87−5999=2899
Step 4: Combine the results
Now, we combine the integer part and the fractional part:
1+2899
This can be expressed as:
1.28¯¯¯¯¯¯28
Thus, the final answer is:
1.28
The notation 3.87¯¯¯¯¯¯87 means that the digits "87" repeat indefinitely. Therefore, we can express it as:
3.87¯¯¯¯¯¯87=3+0.87¯¯¯¯¯¯87
Similarly, for 2.59¯¯¯¯¯¯59:
2.59¯¯¯¯¯¯59=2+0.59¯¯¯¯¯¯59
To convert 0.87¯¯¯¯¯¯87 into a fraction, we can set:
x=0.87¯¯¯¯¯¯87
Then, multiplying by 100 (to shift the decimal point two places to the right):
100x=87.87¯¯¯¯¯¯87
Now, subtracting the original x:
100x−x=87.87¯¯¯¯¯¯87−0.87¯¯¯¯¯¯87
This simplifies to:
99x=87
Thus:
x=8799=2933
So, we have:
0.87¯¯¯¯¯¯87=2933
Let:
y=0.59¯¯¯¯¯¯59
Then, multiplying by 100:
100y=59.59¯¯¯¯¯¯59
Subtracting the original y:
100y−y=59.59¯¯¯¯¯¯59−0.59¯¯¯¯¯¯59
This simplifies to:
99y=59
Thus:
y=5999
Now substituting back into the original expression:
3.87¯¯¯¯¯¯87−2.59¯¯¯¯¯¯59=(3+2933)−(2+5999)
This simplifies to:
(3−2)+(2933−5999)
Calculating 2933−5999:
To subtract these fractions, we need a common denominator. The least common multiple of 33 and 99 is 99. Thus, we convert 2933:
2933=29×333×3=8799
Now we can perform the subtraction:
8799−5999=87−5999=2899
Now, we combine the integer part and the fractional part:
1+2899
This can be expressed as:
1.28¯¯¯¯¯¯28
Thus, the final answer is:
1.28
Topper's Solved these Questions
Similar Questions
Knowledge Check
If 3A = 2B = C, then A : B : C = ?
A. 6 : 2 : 3
B. 1/3 : 1/2 : 1
C. 3 : 2 : 1
D. 1 : 3 : 2AABCCDDB
Match the following.
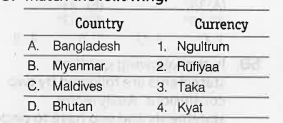
Codes A B C D
(A) 4 3 1 2 (B) 2 4 1 3 (C) 3 4 2 1 (D) 3 4 1 2
View SolutionIf the volumes of two cubes are in the ratio 27 : 1, the ratio of their edges is (a) 1 : 3 (b) 1 : 27 (c) 3 : 1 (d) 27 : 1
View SolutionFill in he blanks :
(a) 369÷=369
(b) (−75)÷=−1
(c) (−206)÷=1
(d) −87÷=87
(e) [_?]÷1=−87
(f) [_]÷48=−1
(g) 20÷=−2
(h) [_]÷(4)=−3
View SolutionThe average of X1, X2 and X3 is 14. Twice the sum of X2 and X3 is 30. What is the value of X1 ? (a) 12 (b) 16 (c) 20 (d) 27
View Solution⎡⎣{(−13)2}−2⎤⎦−1 = (a) 181 (b) 19 (c) −181 (d) −19
View Solution(833.25−384.45)÷24=? (a) 1.87 (b) 2.01 (c) 18.7 (d) 20.1 (e) None of these
View SolutionIf a:(b+c)=1:3 and c:(a+b)=5:7, the b:(a+c) is equal to 1:2 b. 1:3 c. 2:3 d. 2:1
View Solution
