A rectangular park 60 m long and 40 m wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 sq. m, then what is the width of the road? (a) 2.91m (b) 3m (c) 5.82m (d) None of these
To find the width of the road in the rectangular park, we can follow these steps:
Step 1: Calculate the area of the rectangular park
The area of the rectangular park can be calculated using the formula:
Area=Length×Width
Given that the length is 60 m and the width is 40 m, we have:
Area=60m×40m=2400m2
Step 2: Set up the equation for the area of the lawn
Let x be the width of the road. There are two crossroads: one running horizontally and the other vertically. The area of the two crossroads can be calculated as follows:
- The area of the horizontal crossroad: Width×Length=x×40
- The area of the vertical crossroad: Width×Length=x×60
However, the area where the two crossroads intersect (which is counted twice) must be added back. The area of the intersection is:
Area of intersection=x×x=x2
Thus, the total area of the crossroads is:
Area of crossroads=(x×40)+(x×60)−(x2)=100x−x2
Step 3: Express the area of the lawn
The area of the lawn can be expressed as:
Area of lawn=Area of park−Area of crossroads
Given that the area of the lawn is 2109 m², we can write:
2109=2400−(100x−x2)
Step 4: Rearrange the equation
Rearranging the equation gives:
2109=2400−100x+x2
x2−100x+(2400−2109)=0
x2−100x+291=0
Step 5: Solve the quadratic equation
We can solve the quadratic equation x2−100x+291=0 using the factorization method or the quadratic formula. The factors of this equation are:
(x−97)(x−3)=0
Thus, the solutions are:
x=97orx=3
Step 6: Determine the valid solution
Since the width of the road must be less than the dimensions of the park, we reject x=97 and accept:
x=3
Conclusion
The width of the road is 3m.
The area of the rectangular park can be calculated using the formula:
Area=Length×Width
Given that the length is 60 m and the width is 40 m, we have:
Area=60m×40m=2400m2
Let x be the width of the road. There are two crossroads: one running horizontally and the other vertically. The area of the two crossroads can be calculated as follows:
- The area of the horizontal crossroad: Width×Length=x×40
- The area of the vertical crossroad: Width×Length=x×60
Area of intersection=x×x=x2
Area of crossroads=(x×40)+(x×60)−(x2)=100x−x2
The area of the lawn can be expressed as:
Area of lawn=Area of park−Area of crossroads
Given that the area of the lawn is 2109 m², we can write:
2109=2400−(100x−x2)
Rearranging the equation gives:
2109=2400−100x+x2
x2−100x+(2400−2109)=0
x2−100x+291=0
We can solve the quadratic equation x2−100x+291=0 using the factorization method or the quadratic formula. The factors of this equation are:
(x−97)(x−3)=0
Thus, the solutions are:
x=97orx=3
Since the width of the road must be less than the dimensions of the park, we reject x=97 and accept:
x=3
The width of the road is 3m.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A rectangular park 60 metre long and 40 mete wide has concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109metre2 then the width of the road is
A3 metreB5 metreC6 metreD2 metreA rectangular park is 100 m long and 60 m wide. There is a path 2 m wide out side the park. Find the area of the path?
A324m2B656m2C675m2D780m2A rectangle park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.
A200m2B300m2C400m2D375m2
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, then find the area of the road.

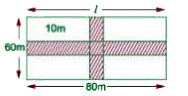
View SolutionA rectangular grass plot 80m×60m has two roads, each 10 m wide, running in the middle of it, one parallel to length and the other parallel to breadth.Find the area of the roads.
View SolutionA rectangular flower garden 20m by 15m has a 3m wide path running in the middle. Find the area of the path.
View SolutionA rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View SolutionA rectangular grass plot 80m×60m has two roads, each 10 m wide, running in the middle of it, one parallel to length and the other parallel to breadth.Find the area of the roads.

View Solution
