A square and a rectangle have equal areas. If their perimeters are p1 and p2 respectively, then (a) p1<p2 (b) p1=p2 (c) p1>p2 (d) None of these
To solve the problem, we need to establish the relationship between the perimeters of a square and a rectangle that have equal areas.
Step 1: Define the areas of the square and rectangle.
Let the side of the square be s. Therefore, the area of the square As is given by:
As=s2
Let the length and breadth of the rectangle be l and b respectively. The area of the rectangle Ar is given by:
Ar=l×b
Since the areas are equal, we have:
s2=l×b(1)
Step 2: Calculate the perimeters of the square and rectangle.
The perimeter p1 of the square is given by:
p1=4s
The perimeter p2 of the rectangle is given by:
p2=2(l+b)
Step 3: Express s in terms of l and b.
From equation (1), we can express s as:
s=√l×b
Step 4: Substitute s into the perimeter of the square.
Now, substituting s into the expression for p1:
p1=4s=4√l×b
Step 5: Relate p1 and p2.
Now we need to compare p1 and p2:
p2=2(l+b)
To compare p1 and p2, we can use the Arithmetic Mean-Geometric Mean (AM-GM) inequality, which states that for any two non-negative numbers l and b:
l+b2≥√l×b
Multiplying both sides by 2 gives:
l+b≥2√l×b
Now, multiplying both sides by 2 gives:
2(l+b)≥4√l×b
This implies:
p2≥p1
Step 6: Conclusion.
Since p2 is greater than or equal to p1, we conclude that:
p1<p2
Thus, the correct answer is:
(a) p1<p2
Let the side of the square be s. Therefore, the area of the square As is given by:
As=s2
Ar=l×b
s2=l×b(1)
The perimeter p1 of the square is given by:
p1=4s
p2=2(l+b)
From equation (1), we can express s as:
s=√l×b
Now, substituting s into the expression for p1:
p1=4s=4√l×b
Now we need to compare p1 and p2:
p2=2(l+b)
l+b2≥√l×b
l+b≥2√l×b
2(l+b)≥4√l×b
p2≥p1
Since p2 is greater than or equal to p1, we conclude that:
p1<p2
(a) p1<p2
Topper's Solved these Questions
Similar Questions
Knowledge Check
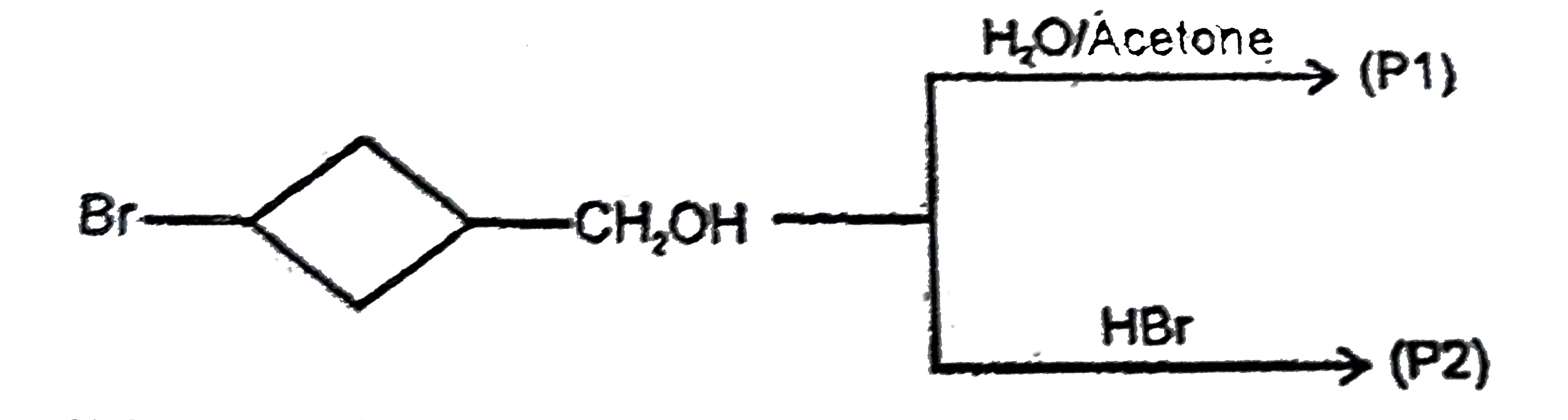
P1 and P2 are respectively :A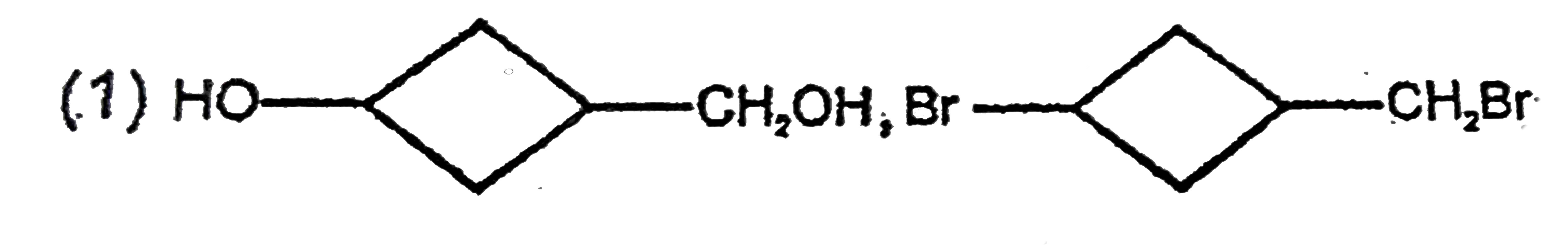 B
B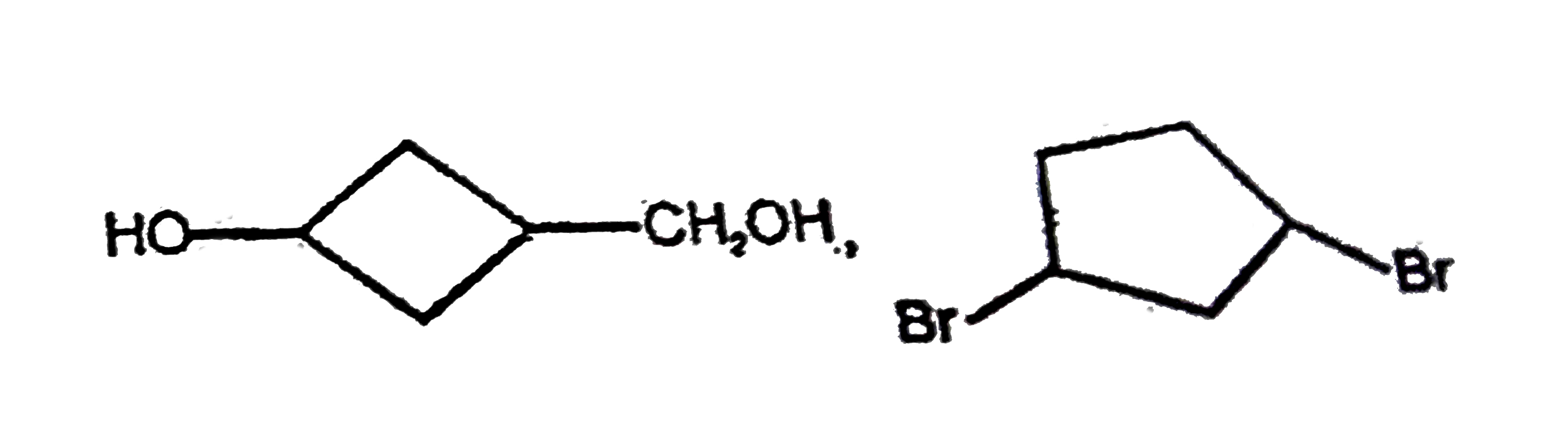 C
C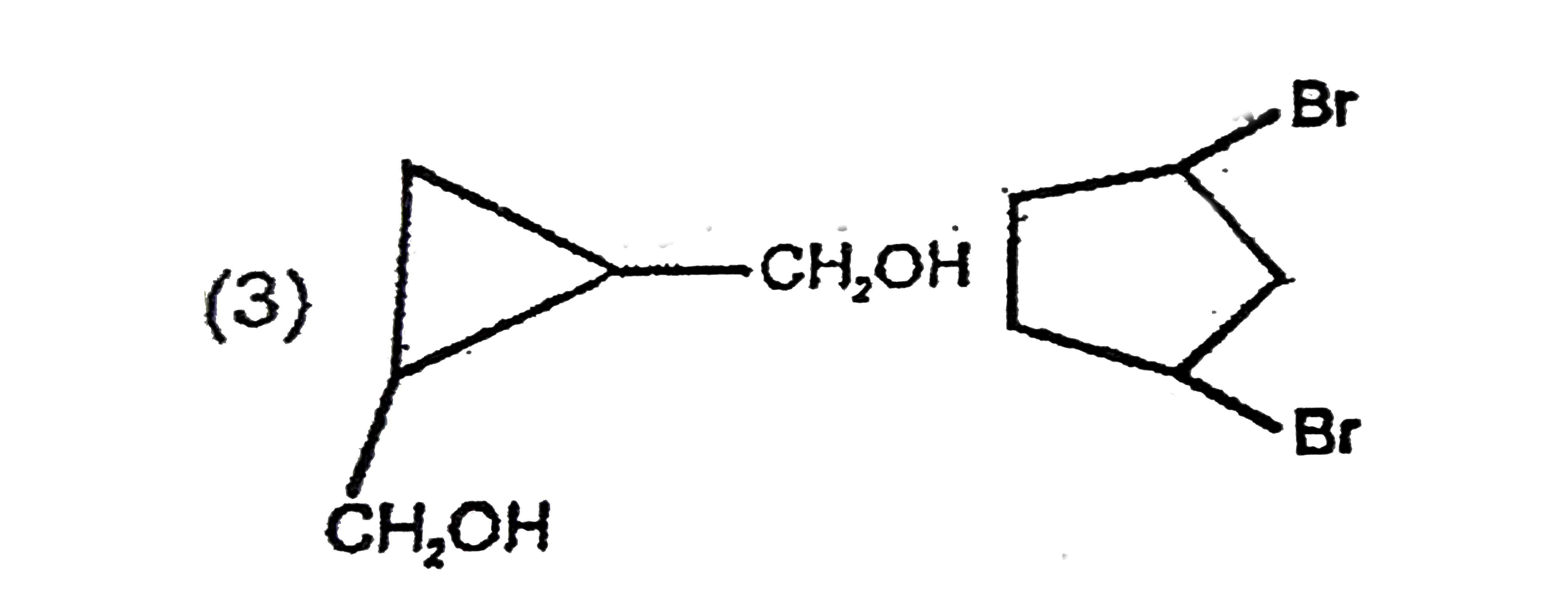 D
D
Two bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
Am1:m2Bm2:m1C√m1:√m2Dm21:m22Three identical conducting plates P1,P2 and P3 are kept at a distance d from each other. If q,-q,2q are the charges in P1,P2 and P3 respectively, the electric field between P1 and P2 is (where A is area of plate)
A(q2Aε0)B(2q2Aε0)C0D(4q2Aε0)
If p1and p2 are the lengths of te perpendiculars from the origin upon the lines x secθ+hycosecθ=a and xcosθ−ysinθ=acos2θ respectively, then 4p12+p22=a2 b. p12−4p22=a2 c. p12+p22=a2 d. none of these
View SolutionConsider a triangle ABC, G be the centroid , AB = c, BC= a, AC = b, p,q,r are the length of the angle bisectors of A,B,C respectively and p1,p2,p3 are the length of the Altitudes from vertices A,B,C respectively: Find 1. Value of √p−21+p−22+p−23 ( Δ denotes area of triangle) is 2. The value ofGA2+GB2+GC2 is 3. The value of 1pcos(A2)+1qcos(B2)+1rcos(C2) is
View SolutionIf p1,p2,p3 re the altitudes of the triangle ABC from the vertices A, B and C respectivel. Prove that cosAp1+cosBp2+cosCp3=1R
View SolutionTwo bodies of masses m1andm2 have equal kinetic energies. If P1 and P2 are their respective momentum, then ratio P1:P2 is equal to
View SolutionTwo bodies of masses m1andm2 have equal kinetic energies. If P1andP2 are their respective momentum, then ratio P1:P2 is equal to
View Solution
