वृत्त में चाप की लम्बाई एवं त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिनके केन्द्रीय कोण व त्रिज्या क्रमश: 60∘ व 6 सेमी. हैं।
Step by step video & image solution for वृत्त में चाप की लम्बाई एवं त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिनके केन्द्रीय कोण व त्रिज्या क्रमश: 60^(@) व 6 सेमी. हैं। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
सही विकल्प चुनकर लिखिए -
जब a1a2≠b1b2 तो समीकरण निकाय a1x+b1y+c1=0 तथा a2x+b2y+c2=0
View Solution96 और 404 का HCF होगा-
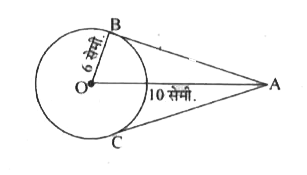
View Solutionदिये गये चित्र में O वृत्त का केंद्र है। AB व AC वृत्त कि स्पर्श रेखाएं है। यदि OA=10 सेमी तथा OB=6 सेमी है तो AC कि लम्बाई लिखिए।
View Solutiony = |x|, x= - 3, x = 1 व x-अक्ष से परिबध्द क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवृत्त की स्पर्श रेखा व त्रिज्या में क्या सम्बन्ध होता है ?
View Solutionएक2.7 सेमी त्रिज्या लेकर वृत्त की रचना कीजिए। उस वृत्त पर एक स्पर्श रेखा खींचिए।
View Solutionवृत्त की स्पर्श रेखा व त्रिज्या में क्या सम्बन्ध होता है ?
View Solutionकिसी बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखा की लम्बाई 12 सेमी है ,यदि वृत्त की त्रिज्या 5 सेमी तो केंद्र से बाह्य बिंदु की दुइ ज्ञात कीजिए।
View Solutionखण्ड 'अ'खण्ड 'ब'1.r त्रिज्या वाले वृत्त का परिमाप(a)14πr22.अर्धवृत्त का क्षेत्रफल(b)2πr3.चतुर्थांश का क्षेत्रफल(c)12πr24.एक मिनट की सुई के द्वारा बनाया गया कोण(d)θ360×2πr5.वृत्त खंड के चाप को लम्बाई(e)6∘
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक वृत्त का केंद्र (2x−1,3x+1) है। x ज्ञात कीजिए यदि वृत्त (-3,-1) में से गुजरे और व्यास की लम्बाई 20 मात्रक हो।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionSeries Jeet|Bihar Board Special#!#वृत्त का क्षेत्रफल#!#त्रिज्य खंड एवं वृत्त खंड का क्षेत्रफल#!#बिहार बोर्ड की परीक्षाओ में आये हुए प्रश्न#!#Revision
View Solutionरेखाएँ एवं कोण|समांतर रेखा व तिर्यक रेखा#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#घन व घनाभ का पृष्ठीय क्षेत्रफल#!#परीक्षा की लिए महत्वपूर्ण अध्याय
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#घन व घनाभ का पृषठीय क्षेत्रफल#!#परीक्षा की द्रष्टी से महत्वपूर्ण प्रश्न
View Solution
