In the given figure, ABC is an equilateral triangle which is inscribed inside a circle and whose radius is r . Which of the following is the area of the triangle? (r+DE)12(r−DE)32 (b) (r−DE)12(r+DE)2 (c) (r−DE)2(r+DE)2 (d) (r−DE)12(r+DE)32
Step by step video & image solution for In the given figure, A B C is an equilateral triangle which is inscribed inside a circle and whose radius is r . Which of the following is the area of the triangle? (r+D E)^(1/2)(r-D E)^(3/2) (b) (r-D E)^(1/2)(r+D E)^2 (c) (r-D E)^2(r+D E)^2 (d) (r-D E)^(1/2)(r+D E)^(3/2) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the given figure, ABC is an equilateral triangle which is inscribed inside a circle and whose radius is r . Which of the following is the area of the triangle? (r+DE)12(r−DE)32 (b) (r−DE)12(r+DE)2 (c) (r−DE)2(r+DE)2 (d) (r−DE)12(r+DE)32
View Solutionif (a,b),(c,d),(e,f)are the vertices of a triangle such that a,c,e are in GP. with common ratio r and b,d,f are in GP with common ratio s, then the area of the triangle is
View SolutionArea of the triangle with vertces (a,b),(x1,y1) and (x2,y2) where a,x1,x2 are in G.P with common ratio r and b,y1,y2 are in G.P with common ratio s is
View SolutionIf (a,b),(c,d),(e,f) are the vertices of a triangle such that a, c, e are in G. P. with common ratio r and b, d, f are in G. P. with common ratio s, then the area of the triangle is
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
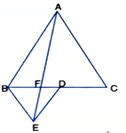
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)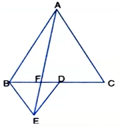
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
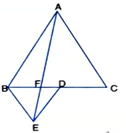
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BFE)=ar(AFD)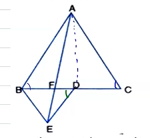
View SolutionDifferentiate the following w.r.t. as indicated :
e2x w.r.t. ex
View Solution
