A right circular cone is divided into two portions by a plane parallel to the base and passing through a point which is 13rd of the height from the top. The ratio of the volume of the smaller cone to that of the remaining frustum of the cone is (a) 1 : 3 (b) 1 : 9 (c) 1 : 26 (d) 1 : 27
To solve the problem, we need to find the ratio of the volume of the smaller cone to that of the remaining frustum of the cone when a right circular cone is divided by a plane parallel to the base at a height of 13h from the top.
Step 1: Define the dimensions of the cone
Let the radius of the base of the cone be r and the height of the cone be h.
Hint: Identify the dimensions of the cone clearly to set up the problem.
Step 2: Determine the height of the smaller cone
The height of the smaller cone, which is formed above the plane, is 13h (since the plane is at 13 of the height from the top).
Hint: Remember that the height of the smaller cone is a fraction of the total height.
Step 3: Find the radius of the smaller cone
Since the smaller cone is similar to the original cone, we can find the radius of the smaller cone using the ratio of the heights. The radius of the smaller cone r1 is given by:
r1=13r
Hint: Use the property of similar triangles to find the radius of the smaller cone.
Step 4: Calculate the volume of the smaller cone
The volume V1 of the smaller cone can be calculated using the formula for the volume of a cone:
V1=13πr21h1=13π(13r)2(13h)
Substituting r1 and h1:
V1=13π(13r)2(13h)=13πr29h3=181πr2h
Hint: Use the volume formula and substitute the dimensions correctly.
Step 5: Calculate the volume of the original cone
The volume V of the original cone is:
V=13πr2h
Hint: Recall the formula for the volume of a cone.
Step 6: Calculate the volume of the frustum
The volume of the frustum Vf is the volume of the original cone minus the volume of the smaller cone:
Vf=V−V1=13πr2h−181πr2h
To combine these, we need a common denominator:
Vf=2781πr2h−181πr2h=2681πr2h
Hint: Make sure to perform the subtraction carefully, keeping track of the common denominators.
Step 7: Find the ratio of the volumes
Now we can find the ratio of the volume of the smaller cone to the volume of the frustum:
Ratio=V1Vf=181πr2h2681πr2h
This simplifies to:
Ratio=126
Thus, the ratio of the volume of the smaller cone to that of the remaining frustum is:
1:26
Final Answer
The correct option is (c) 1 : 26.
---
Let the radius of the base of the cone be r and the height of the cone be h.
The height of the smaller cone, which is formed above the plane, is 13h (since the plane is at 13 of the height from the top).
Since the smaller cone is similar to the original cone, we can find the radius of the smaller cone using the ratio of the heights. The radius of the smaller cone r1 is given by:
The volume V1 of the smaller cone can be calculated using the formula for the volume of a cone:
The volume V of the original cone is:
The volume of the frustum Vf is the volume of the original cone minus the volume of the smaller cone:
Now we can find the ratio of the volume of the smaller cone to the volume of the frustum:
The correct option is (c) 1 : 26.
Topper's Solved these Questions
Similar Questions
A right circular cone is divided by a plane parallel to its base in two equal volumes. In what ratio will the plane divide the axis of the cone?
View SolutionA solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is: 1:2 (b) 1:4 (c) 1:6 (d) 1:8
View Solution
Knowledge Check
A plane parallel to the base of a cone cuts its axis in the ratio 2:1 from its base. The ratio of the volume of the lower part of the cone to that of the upper part is
AA)27:1BB)26:1CC)8:1DD)7:1A right circular cone of height h is cut by a plane parallel to the base and at a distance h/3 from the base, then the volumes of the resulting cone and frustum are in the ratio
A1:3B8:19C1:4D1:7A right circular cone is divided into 3 portions A<<B and C by planes parallel to the base as shown in the figure.
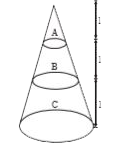
The height of each portion is 1 unit. calculate.
(1) the ratio of the volume of A to the volume of B.
(2) the ratio of the volume of B to that C.A1 : 7, 7 : 19B1 : 7, 19 : 7C1 : 8, 19 : 7D1 : 7, 8 : 19
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
View SolutionA right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7: 19.
View SolutionIf the height of a cone is doubled and its base diameter is trebled, then the ratio of the volume of the resultant cone to that of the original cone is (a) 6 : 1 (b) 9 : 1 (c) 9 : 2 (d) 18 : 1
View SolutionA solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base . The ratio of the volume of the smaller cone to the whole cone is
View SolutionA cone of radius r сm and height h cm is divided into two parts by drawing a plane through the middle point of its height and parallel to the base. What is the ratio of the volume of the original cone to the volume of the smaller cone?
View Solution