A segment of a line PQ with its extremities on ABandAC bisects a triangle ABC with sides a,b,c into two equal areas. Find the shortest length of the segment PQ.
Step by step video & image solution for A segment of a line P Q with its extremities on A Ba n dA C bisects a triangle A B C with sides a ,b ,c into two equal areas. Find the shortest length of the segment P Qdot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Let A(1,0),B(6,2) and C(32,6) be the vertices of a triangle ABC. If P is a point inside the triangle ABC such that the triangles APC, APB and BPC have equal areas , then the length of the line segment PQ, where Q is the point (−76,−13), is _________.
View SolutionLet A(5,−3),B(2,7)andC(−1,2) be the vertices of a △ABC. If P is a point inside the triangle ABC such that the triangle APC,APB and BPC have equal areas, then length of the line segment PB is:
View Solution
Knowledge Check
A triangle has sides of length 6, 7 and 8. The line through its incenter parallel to the shortest side is drawn to meet the other two sides at P and Q. The length of the segment PQ is
A125B154C307D339If in ΔABC, sides a, b, c are in A.P. then
AB>60∘BB<60∘CB≤60∘DB=|A−C|
Let A(5,-3), B(2,7) and C(-1,2) be the vertices of a triangle A,B,C. If P is a point inside the triangle ABC such that the triangle APC,APB and BPC have equal areas, then length of the line segment PB is:
View SolutionSides of triangle ABC are in A.P. if a<min{b,c} then cosA is equal to
View SolutionIf the sides a,bandc of a triangle ABC are in A.P. then bc belongs to
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
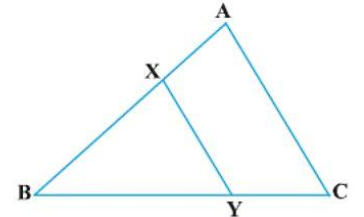
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View SolutionA triangle has sides 6,7, and 8. The line through its incenter parallel to the shortest side is drawn to meet the other two sides at P and Q. Then find the length of the segment PQ.
View Solution
