If E1,E2, are two events with E1∩E2=ϕ then P(¯¯¯E1∩¯¯¯E2)=
Step by step video & image solution for If E_1, E_2, are two events with E_1 nn E_2 = phi then P(bar E_1 nn bar E_2) = by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Statement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1AStatement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for statement -9BStatement-1 is true, Statement-2 is true, Statement-2 is Not a correct explanation for statement -9CStatement-1 is true, Statement-2 is FalseDStatement-1 is False, Statement-2 is trueFor any two independent events E1andE2,P{(E1∪E2)∩(¯¯¯E1∩¯¯¯E2)} is
A<14B>14C≥12DNone
Statement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1
View SolutionIf E1,E2,E3 are independent events, such that P(E1∩¯¯¯¯E2∩¯¯¯¯E3)=14,P(¯¯¯¯E1∩¯¯¯¯E2∩¯¯¯¯E3)=18,P(¯¯¯¯E1∩E2∩¯¯¯¯E3)=18. Find P(¯¯¯¯E3)
View SolutionLet E1 and E2 be the events such that P(E1)=13 and P(E2)=35.
Find :
(i) P(E1∪E2), where E1 and E2 are mutually ecclusive,
(ii) P(E1∩E2), when E1 and E2 are independent.
View SolutionSuppose E1 and E2 are two events of a sample space such that P(E1)=12,P(E2∣E1)=12,P(E1∣E2)=14 then P(E'2)= _____
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
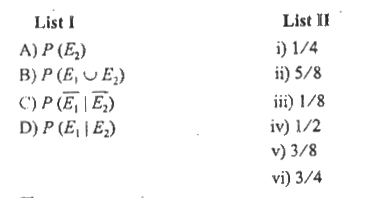
The correct matching of the list I from the list II is :
View SolutionIf E1 and E2 are the two events such that P(E1)=14,P(E2)=13 and P(E1∪E2)=12, show that E1 and E2 are independent events.
View Solution
