If L1&L2 are the lengths of the segments of any focal chord of the parabola y2=x, then (a) 1L1+1L2=2 (b) 1L1+1L2=12 (c) 1L1+1L2=4 (d) 1L1+1L2=14
Step by step video & image solution for If L_1&L_2 are the lengths of the segments of any focal chord of the parabola y^2=x , then (a) 1/(L_1)+1/(L_2)=2 (b) 1/(L_1)+1/(L_2)=1/2 (c) 1/(L_1)+1/(L_2)=4 (d) 1/(L_1)+1/(L_2)=1/4 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If L1&L2 are the lengths of the segments of any focal chord of the parabola y2=x, then (a) 1L1+1L2=2 (b) 1L1+1L2=12 (c) 1L1+1L2=4 (d) 1L1+1L2=14
View SolutionLet L1 be the length of the common chord of the curves x2+y2=9 and y2=8x, and L2 be the length of the latus rectum of y2=8x, then: (A) L1<L2 (B) L1L2=√2 (C) L1>L2 (D) L1=L2
View Solution
Knowledge Check
If l1 and l2 are lengths of two perpendicular focal chord of parabola y2=16(x+1), then harmonic mean of l1 and l2 is:
A4B8C16D32The area of triangle formed by the lines l1andl2 and the x-axis is:
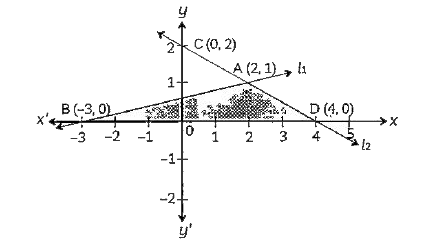 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. unitsIf L1=(2.02±0.01)m and L2=(1.02±0.01)m then L1+2L2 is (in m)
A4.06±0.02B4.06±0.03C4.06±0.005D4.065±0.01
If L1andL2, are the length of the tangent from (0, 5) to the circles x2+y2+2x−4=0andx2+y2−y+1=0 then
View SolutionThe chord of contact of tangents from a point P to a circle passes through Q. If l1andl2 are the length of the tangents from PandQ to the circle, then PQ is equal to l1+l22 (b) l1−l22 √l12+l22 (d) 2√l12+l22
View SolutionIf a rectangle has length L and the width is one-half of the length, then the area of the rectangle is (a) L (b) L2 (c) 12L2 (d) 14L2 (e) 2L
View SolutionIf c is small in comparision with l then (ll+c)12+(ll−c)12=
View SolutionExplain , giving reason , which of the following sets of quantum number are not possible an=0l=0m1=0ms=+1/2bn=1l=0m1=0ms=−1/2cn=1l=1m1=0ms=+1/2dn=2l=1m1=0ms=−1/2en=3l=3m1=−3ms=+1/2fn=3l=1m1=0ms=+1/2
View Solution