Question

वैधुत परिपथ सम्बन्धी किरचॉफ के नियमो को उदाहरण देकर स्पष्ट कीजिए।

Explanation

किरचॉफ के वैधुत परिपथ सम्बन्धी नियम-
प्रथम नियम (सन्धि अथवा धारा का नियम )-"किसी वैधुत परिपथ में किसी भी सन्धि (जोड़) पर मिलने वाली समस्त धाराओं को बीजगणितीय योग शून्य होता है। " अर्थात `sumi=0`
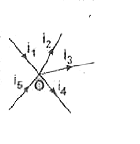
माना किसी परिपथ में धाराएँ `i_(1),i_(2),i_(3),i_(4)` व `i_(5)` बह रही है, जो सन्धि `O` पर मिल रही है। चिह परिपाटी के अनुसार सन्धि की ओर आने वाली धाराएँ धनात्मक तथा सन्धि से दूर जाने वाली धाराएँ ऋणात्मक ली जाती है , अतः `i_(1)` व `i_(5)` धनात्मक तथा `i_(2),i_(3)` व `i_(4)` ऋणात्मक होगी , अतः किरचॉफ के नियमानुसार,
`i_(1)+i_(5)-i_(2)-i_(3)-i_(4)=0`
अथवा `i_(1)+i_(5)=i_(2)+i_(3)+i_(4)`

अतः वैधुत परिपथ की किसी सन्धि पर आने वाली सब धाराओं का योग, उस सन्धि से दूर जाने वाली सब धाराओं के योग के बराबर होता है। इस प्रकार यह नियम आवेश के सरंक्षण को व्यक्त करता है , इसलिए इसे किरचॉफ का धारा नियम भी कहते है।
द्वितीय नियम (वोल्टता अथवा पाश का नियम)- "किसी वैधुत परिपथ में प्रत्येक बन्द पाश के विभिन्न खण्डों में प्रवाहित होने वाली धारा एवं उनके संगत प्रतिरोधों के गुणनफलो का बीजगणितीय योग उस पाश में कार्य करने वाले समस्त वैधुत वाहक बलों के बीजगणितीय योग के बराबर होता है। "
अर्थात `sumiR=sumE`
सल्गन चित्र के वैधुत परिपथ में दो बन्द पाश `(1)` व `(2)` है। इस वैधुत परिपथ में दो सेलो जिनके वैधुत वाहक बल व है तथा तीन प्रतिरोधों व को परस्पर जोड़ा गया है। माना प्रतिरोधों व में प्रवाहित धाराएँ क्रमश : व है जो सेलो व से प्राप्त होती है। सन्धि पर किरचॉफ का प्रथम नियम लगाने से , प्रतिरोध में प्रवाहित में प्रवाहित धारा होगी, अतः बन्द पाश में किरचॉफ के द्वितीय नियम से,

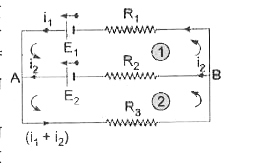
`i_(1)R_(1)-i_(2)R_(2)=E_(1)-E_(2)`
तथा बन्द पाश `(2)` के लिए,
`i_(2)R_(2)+(i_(1)+i_(2))R_(3)=E_(2)`
इन समीकरणों को हल करके `i_(1)` व `i_(2)` के मान ज्ञात किए जा सकते है। इस प्रकार यह नियम ऊर्जा के सरंक्षण को व्यक्त करता है , इसीलिए इस किरचॉफ को वोल्टता नियम भी कहते है।