एक अनन्त लम्बे तार धारावाही चालक a मीटर की दूरी पर चुम्बकीय क्षेत्र के लिए व्यंजक प्राप्त कीजिए।
Video Solution
Text Solution
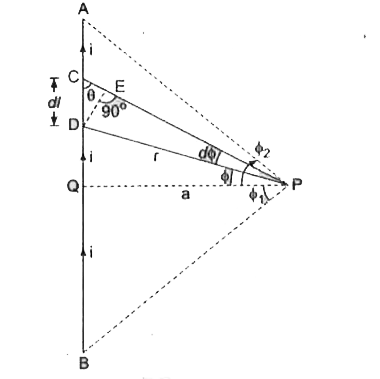
परिमित लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र - माना L लम्बाई के एक सीधे चालक AB में i ऐम्पियर की धारा बाह रही है। इस चालक के समीप कोई बिन्दु P है, जहाँ चुम्बकीय क्षेत्र B ज्ञात करना है। बिन्दु P से चालक AB पर लम्ब PQ है जिसकी लम्बाई a है माना चालक AB का अल्पांश भाग CD है जिसकी बिन्दु P से दूरी r तथा CD=dl है। माना ∠DPQ=ϕ तथा ∠CPD=dϕ | माना ∠DCP=θ तथा DE.CP पर लम्ब है।
बायो - सावर्ट के नियम से, अल्पांश dl के कारण बिन्दु P पर चुम्बकीय क्षेत्र
dB=μ04π⋅sinθr2
पुनः ΔCDE में, sinθ=DECD
अतः DE=cDsinθ=dlsinθ
∵DE, बिन्दु P पर dϕ कोण अन्तरित करती है।
∴dϕ (रेडियन में) =DEDP=DEr अथवा DE=rdϕ
अतः alsinθ=rdϕ
तथा ΔDPQ में cosϕ=ar, अतः r=acosϕ
∴ dB=μ04π⋅irdϕr2=μ04π⋅idϕr
अथवा dB=μ04π⋅icosϕdϕa
माना ∠BPQ=ϕ1 तथा ∠APQ=ϕ2
चूँकि ϕ1 व ϕ2 लम्ब PQ से विपरीत दिशाओं में नापे जा रहे है, अतः ϕ1 ऋणात्मक व ϕ2 धनात्मक होगा |
अतः सम्पूर्ण चालक AB के कारण बिन्दु P पर चुम्बकीय क्षेत्र
B=∫ϕ2−ϕ1μ04π⋅icosϕdϕa=μ04π⋅ia∫ϕ2−ϕ1=μ04π⋅ia∫ϕ2−ϕ1cosϕ.dϕ[∵μ04π⋅ia= नियतांक]
=μ04π⋅ia[sinϕ]ϕ2−ϕ1=μ04π⋅ia[sinϕ2−sin(−ϕ1)]
=μ04π⋅ia(sinϕ1+sinϕ2)
दाएँ हाथ की हथेली के नियम 1 से, चुम्बकीय क्षेत्र B की दिशा कागज़ के तल के लम्बत नीचे की ओर होगी।
विशेष स्थितियाँ -
1. यदि चालक बिन्दु P के दोनों ओर अनन्त दूरी तक जाता है तो
ϕ1=ϕ2=90∘
तब, B=μ04π⋅ia[sin90∘+sin90∘]
=μ04π⋅2ia=μ02π⋅ia न्यूटन/(ऐम्पियर - मीटर) ।
यह अपरिमित लम्बाई के ऋजुरेखीय धारावाही चालक के कारण चुम्बकीय क्षेत्र का सूत्र है।
2. यदि बिन्दु P अपरिमित लम्बाई के चालक के सिरे A के समीप तथा चालक से a दूरी पर है तो ϕ1≅π/2 तथा ϕ2≅0
अतः B=μ04π⋅ia न्यूटन/(ऐम्पियर - मीटर) ।
|
Similar Questions
एक समान चुम्बकीय क्षेत्र मे धारावाही चालक
View Solutionएक समान चुम्बकीय क्षेत्र मे धारावाही चालक
View Solutionधारावाहि चालक तार पर चुम्बकीय क्षेत्र के कारण लगने वाला बल
View Solutionसीधे धारावाही चालक तार के कारण चुम्बकीय क्षेत्र
View Solutionसीधे धारावाही तार के कारण चुम्बकीय क्षेत्र
View Solutionसीधे लम्बे धारावाही चालक के कारण चुम्बकीय क्षेत्र#!#धारावाही वृताकार लूप के केंद्र पर चुंबकीय क्षेत्र
View Solutionपतले सीधे धारावाही चालक के चारो ओर चुम्बकीय क्षेत्र |धारावाही वृतीय चाप के केंद्र पर चुम्बकीय क्षेत्र |विद्युत धारावाही वृताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही चालक के कारण चुम्बकीय क्षेत्रधारावाही चालक के कारण चुम्बकीय क्षेत्र|ऐम्पियर का परिपथीय नियम|विद्युत धारावाही चालक पर चुम्बकीय बल
View Solution
