बायो-सावर्ट के नियम की सहायता से अनन्त लम्बाई के धारावाही चालक के कारण r दूरी पर उतपन्न चुम्बकीय क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
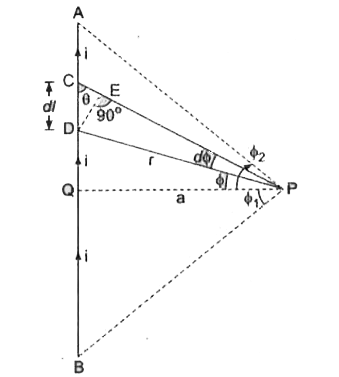
परिमित लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र - माना L लम्बाई के एक सीधे चालक AB में i ऐम्पियर की धारा बाह रही है। इस चालक के समीप कोई बिन्दु P है, जहाँ चुम्बकीय क्षेत्र B ज्ञात करना है। बिन्दु P से चालक AB पर लम्ब PQ है जिसकी लम्बाई a है माना चालक AB का अल्पांश भाग CD है जिसकी बिन्दु P से दूरी r तथा है। माना तथा | माना तथा पर लम्ब है।
बायो - सावर्ट के नियम से, अल्पांश के कारण बिन्दु P पर चुम्बकीय क्षेत्र
पुनः में,
अतः
, बिन्दु P पर कोण अन्तरित करती है।
(रेडियन में) अथवा
अतः
तथा में , अतः
अथवा
माना तथा
चूँकि व लम्ब से विपरीत दिशाओं में नापे जा रहे है, अतः ऋणात्मक व धनात्मक होगा |
अतः सम्पूर्ण चालक AB के कारण बिन्दु P पर चुम्बकीय क्षेत्र
दाएँ हाथ की हथेली के नियम 1 से, चुम्बकीय क्षेत्र B की दिशा कागज़ के तल के लम्बत नीचे की ओर होगी।
विशेष स्थितियाँ -
1. यदि चालक बिन्दु P के दोनों ओर अनन्त दूरी तक जाता है तो
तब,
न्यूटन/(ऐम्पियर - मीटर) ।
यह अपरिमित लम्बाई के ऋजुरेखीय धारावाही चालक के कारण चुम्बकीय क्षेत्र का सूत्र है।
2. यदि बिन्दु P अपरिमित लम्बाई के चालक के सिरे A के समीप तथा चालक से a दूरी पर है तो तथा
अतः न्यूटन/(ऐम्पियर - मीटर) ।
Similar Questions
रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता पर आधारित प्रश्न
View Solutionधारावाही चालक तार के कारण चुम्बकीय क्षेत्र
View Solutionसीधे धारावाही चालक तार के कारण चुम्बकीय क्षेत्र
View Solutionसीधे धारावाही तार के कारण चुम्बकीय क्षेत्र
View Solutionधारा का चुम्बकीय प्रभाव #!#ओर्स्टेड का प्रयोग #!#एम्पीयर के तैरने का नियम#!#विधुत धारावाही तार चालक का चुम्बकीय क्षेत्र #!#दाये हाथ का नियम #!#दाये हाथ की हथेली का नियम #!#बायो सेवर्ट का नियम
View Solutionसीधे लम्बे धारावाही चालक के कारण चुम्बकीय क्षेत्र#!#धारावाही वृताकार लूप के केंद्र पर चुंबकीय क्षेत्र
View Solutionपतले सीधे धारावाही चालक के चारो ओर चुम्बकीय क्षेत्र |धारावाही वृतीय चाप के केंद्र पर चुम्बकीय क्षेत्र |विद्युत धारावाही वृताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही चालक के कारण चुम्बकीय क्षेत्रधारावाही चालक के कारण चुम्बकीय क्षेत्र|ऐम्पियर का परिपथीय नियम|विद्युत धारावाही चालक पर चुम्बकीय बल
View Solution
