बायो-सावर्ट के न्यायम की सहायता से किसी धारावाही वृत्ताकार कुंडली अथवा लूप के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र के लिए व्यंजक प्राप्त कीजिए।
Video Solution
Text Solution
वृत्ताकार धारावाही कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र की तीव्रता - माना एक तार को मोड़कर r मीटर त्रिज्या की वृत्ताकार कुण्डली बनाई गई है। जिसमे i ऐम्पियर की धारा प्रवाहित हो रही है। कुण्डली के केन्द्र O पर चुम्बकीय क्षेत्र ज्ञात करने के लिए कुण्डली की परिधि को छोटे - छोटे अल्पांशों में विभाजित किया जा सकता है (चित्र)। माना इनमे से एक अल्पांश की लम्बाई Δl है। बायो-सावर्ट नियम के अनुसार, कुण्डली के केन्द्र O पर चुम्बकीय क्षेत्र
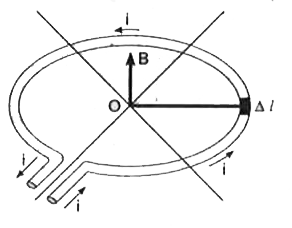
ΔB=μ04π⋅iΔlsinθr2
जहाँ θ अल्पांश Δl तथा अल्पांश को केन्द्र से मिलाने वाली रेखा के बीच का कोण है चूँकि परिधि के प्रत्येक बिन्दु पर त्रिज्या, परिधि के लम्बवत होती है
(θ=90∘)
अतः ΔB=μ04π⋅iΔlsin90∘r2=μ04π⋅iΔlr2
समस्त अल्पांशों द्वारा कुण्डली के केन्द्र O पर उत्पन्न चुम्बकीय क्षेत्र,
B=Σ(ΔB)=Σ(μ04π⋅iΔlr2)=μ04π⋅ir2ΣΔl
परन्तु ΣΔl=2πr (वृत्ताकार कुण्डली की परिधि की लम्बाई)
अतः B=μ04π⋅ir2(2πr)=μ0i2r
|
Similar Questions
विद्युत धारावाही वृत्ताकार पाश के केन्द्र पर चुंबकीय क्षेत्र|आंकीक प्रश्न
View Solutionविद्युत धारावाही वृत्ताकार पाश के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View SolutionRecap|धारावाही लूप के कारण चुम्ब्कीय क्षेत्र
View SolutionRecap|धारावाही कुंडली के अक्ष पर चुम्ब्कीय क्षेत्र
View SolutionRecap|धारावाही कुंडली के अक्ष पर चुम्ब्कीय क्षेत्र|प्रश्न|Summary
View Solutionवृत्ताकार धारावाही कुंडली के अक्ष पर एक बिंदु पर चुंबकीय क्षेत्र
View Solutionधारावाही लूप के कारण चुम्बकीय क्षेत्र
View Solution
