H1 is a regular hexagon circumscribing a circle. H2 is a regular hexagon inscribed in the circle. Find the ratio of areas of H1 and H2
A
4:3
B
2:1
C
3:1
D
3:2
Video Solution
Text Solution
The correct Answer is:A
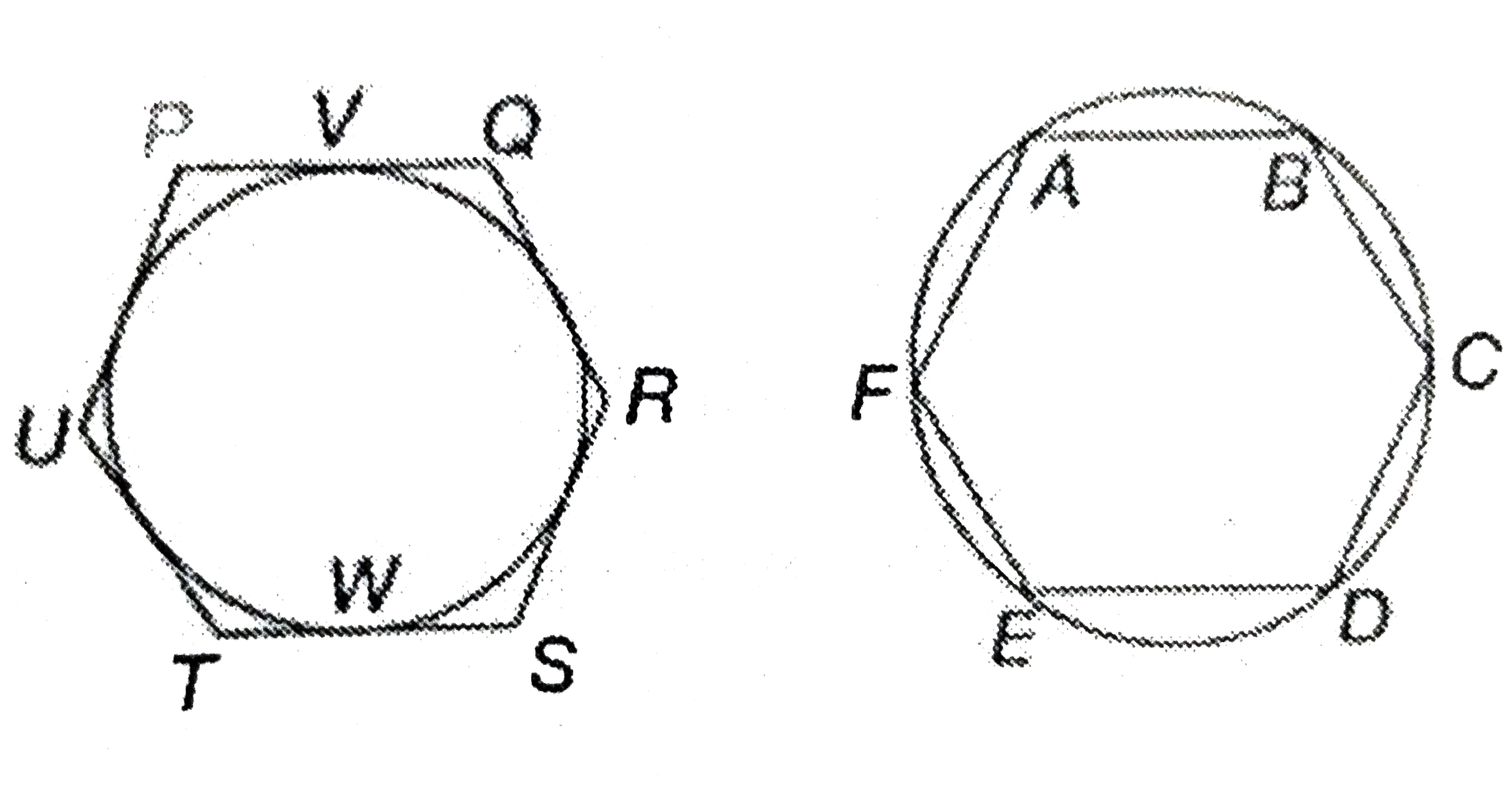
Let H1 be PQRSTU and H2 be ABCDEF.
Let R be the radius of the circle.
∴R=√3(PU)2⇒PU=2R√3
AB=R(∵A hexagon inscribed in a circle must have its side equal to the radius of the circle)
Area of H1=3√32(2√3R)2
And area of H2=3√32(R)2
(∵ Area of hexagon=3√32×(Its side)2)
Required ratio =(2√3R)2R2=43.
|
Topper's Solved these Questions
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Level 2
20 Videos
- MATRICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICESEXERCISE - EXERCISE CONCEPT APPLICATION (LEVEL 3)
15 Videos
- MODULAR ARITHMETIC BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODULAR ARITHMETIC EXERCISE - Level 3
15 Videos
Similar Questions
Knowledge Check
If a regular hexagon circumscribes a circle of radius r , then its perimeter is :
A4√3rB6√3rC6rD12 sqrt3rIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
A4√3rB6√3rC6rD12√3rWhat is the difference in the areas of the regular hexagon circumscribing a circle of radius 10 cm and the regular hexagon inscribed in the circle?
A50cm^(2)B50√3cm2C100√3cm2D100√3cm2
if a regular hexagon and regular octagon are inscribed in a circle of radius R then the ratio of areas A1, and A2, is
View SolutionIf the area of circle is A1 and area of regular pentagon inscibed in the circle is A2, then find the ratio of area of two.
View SolutionWhat is the area of a regular hexagon inscribed in a circle of radius r ?
View SolutionIf a regular hexagon is inscribed in a circle of radius r , then its perimeter is :
View SolutionIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
View Solution
