A question paper contains 20 questions in how many ways can 4 questions be attempted?
To solve the problem of how many ways 4 questions can be attempted from a total of 20 questions, we will use the concept of combinations. This is because the order in which we select the questions does not matter.
1. Identify the total number of questions (n):
We have a total of 20 questions available in the question paper.
n=20
2. Identify the number of questions to be selected (r):
We need to select 4 questions to attempt.
r=4
3. Use the combination formula:
The number of ways to choose r items from n items is given by the combination formula:
C(n,r)=n!r!(n−r)!
In our case, we need to calculate C(20,4).
4. Substitute the values into the formula:
C(20,4)=20!4!(20−4)!=20!4!⋅16!
5. Simplify the factorials:
We can simplify 20! as follows:
20!=20×19×18×17×16!
Thus, we have:
C(20,4)=20×19×18×17×16!4!⋅16!
The 16! cancels out:
C(20,4)=20×19×18×174!
6. Calculate 4!:
4!=4×3×2×1=24
7. Calculate the numerator:
Now calculate the product of the numbers in the numerator:
20×19=380
380×18=6840
6840×17=116280
8. Divide by 4!:
Now divide the result by 4!:
C(20,4)=11628024=4845
Final Answer:
The number of ways to attempt 4 questions from a total of 20 questions is 4845.
---
We have a total of 20 questions available in the question paper.
n=20
We need to select 4 questions to attempt.
r=4
The number of ways to choose r items from n items is given by the combination formula:
C(n,r)=n!r!(n−r)!
In our case, we need to calculate C(20,4).
C(20,4)=20!4!(20−4)!=20!4!⋅16!
We can simplify 20! as follows:
20!=20×19×18×17×16!
Thus, we have:
C(20,4)=20×19×18×17×16!4!⋅16!
The 16! cancels out:
C(20,4)=20×19×18×174!
4!=4×3×2×1=24
Now calculate the product of the numbers in the numerator:
20×19=380
380×18=6840
6840×17=116280
Now divide the result by 4!:
C(20,4)=11628024=4845
The number of ways to attempt 4 questions from a total of 20 questions is 4845.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATION BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PERMUTATIONS AND COMBINATION EXERCISE - Eassy type
5 Videos
- PERMUTATIONS AND COMBINATION BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PERMUTATIONS AND COMBINATION EXERCISE - LEVEL 1
30 Videos
- PERMUTATIONS AND COMBINATION BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PERMUTATIONS AND COMBINATION EXERCISE - Very short ans.
29 Videos
- PARTIAL FRACTIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PARTIAL FRACTIONSEXERCISE - Level-3
10 Videos
- PROGRESSIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PROGRESSIONSEXERCISE - LEVEL 3
18 Videos
Similar Questions
A question paper contain 15 questions. In how many ways can 7 questions be attempted?
View SolutionThere are three sections in a question paper, each containing 5 questions. A candidate has to solve any 5 questions, choosing at least one from each section. Find the number of ways in which the candidate can choose the questions.
View Solution
Knowledge Check
An examination paper consists of 12 questions divided into two parts, part A and part 8. Part A contains 7 questions and part B contains 5 questions. A candidate is required to attempt 8 questions, selecting atleast 3 from each part. In how many ways can he select the questions?
A240B60C420D480An examination paper consists of 12 questions divided into two parts, part A and part 8. Part A contains 7 questions and part B contains 5 questions. A candidate is required to attempt 8 questions, selecting atleast 3 from each part. In how many ways can he select the questions?
A240B60C420D480In a test paper there are 10 questions . Number of ways in which 6 questions to be answered is
A210B540C336Dnone of these
A test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while 14 mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.
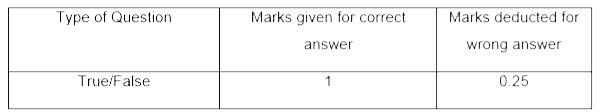
If answer to all questions he attempted by guessing were wrong, then how many questions answered correctly to score 95 marks?
View SolutionA test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while 14 mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.
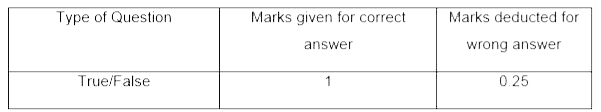
If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly?
View SolutionA paperr consists of 7 questions in part A and 5 questions in part B. A student have to attempt 8 questions. How many ways it can be done if it is necessary to attempt at least three questions from each part ?
View SolutionA question paper consists of two sections having respectively, 3 and 5 questions. The followinng note is given on the paper "it is not necessory to attempt all the questions one questions from each section is compulsory". In how many ways can candidate select the questions?
View SolutionA question paper consists of two sections having respectively 3 and 5 questions. The following note is given on the paper. "It is not necessary to attempt all the questions". One question from each section is compulsory. In how many ways, a candidate can select the question?
View Solution
