Verify, whether D is the mid point of AG.
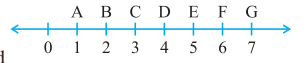
We have, AG=7cm–1cm=6cm
AD=4cm–1cm=3cm
DG=7cm–4cm=3cm
AD+DG=3cm+3cm=6cm
Therefore, AG=AD+DG.
where, AD=DG=3cm
Hence, D is the midpoint of AG
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - UNDERSTANDING ELEMENTARY SHAPESEXERCISE - EXERCISE 5.73videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - NCERTCHAPTER - UNDERSTANDING ELEMENTARY SHAPESEXERCISE - EXERCISE 5.54videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - NCERTCHAPTER - UNDERSTANDING ELEMENTARY SHAPESEXERCISE - EXERCISE 5.92videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - NCERTCHAPTER - SYMMETRYEXERCISE - EXERCISE 13.26videos
SYMMETRY
- BOOK - NCERTCHAPTER - WHOLE NUMBERSEXERCISE - SOLVED EXAMPLES7videos
WHOLE NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
ABC and BDE are two equilateral trainales, such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is :
A1:4B1:2C2:1D4:1 - Question 2 - Select One
Locus of mid point of AB is
Ax2=−2yB2x2=−yCx2=−4yDx22−y21=−1
Find the coordinates of the point R which divides the join of P(0,0,0)andQ(4,−1,−2) in the ratio 1:2 externally and verify that P is the mid point of RQ.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionWe have AC=XD , C is the mid point of AB and D is the mid point of XY, Using Euclid's axiom ,show that AB=XY
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
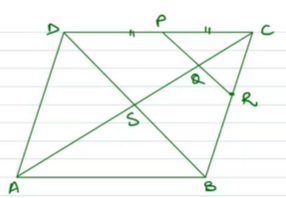
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
 View Solution
View Solution


