Find limx→0f(x), where f(x)={x|x | ,x≠00,x=0
To find the limit of the function f(x) as x approaches 0, we need to analyze the function defined as follows:
f(x)={x|x|if x≠00if x=0
Step 1: Analyze the function for x>0
When x>0, the absolute value |x| is equal to x. Therefore, we can simplify the function:
f(x)=x|x|=xx=1
Step 2: Analyze the function for x<0
When x<0, the absolute value |x| is equal to −x. Thus, we can simplify the function as follows:
f(x)=x|x|=x−x=−1
Step 3: Evaluate the left-hand limit as x approaches 0
We need to find the limit of f(x) as x approaches 0 from the left (denoted as 0−):
limx→0−f(x)=limx→0−(−1)=−1
Step 4: Evaluate the right-hand limit as x approaches 0
Next, we find the limit of f(x) as x approaches 0 from the right (denoted as 0+):
limx→0+f(x)=limx→0+(1)=1
Step 5: Compare the left-hand and right-hand limits
Now we compare the left-hand limit and the right-hand limit:
- Left-hand limit: limx→0−f(x)=−1
- Right-hand limit: limx→0+f(x)=1
Since the left-hand limit is not equal to the right-hand limit:
limx→0−f(x)≠limx→0+f(x)
Conclusion
Thus, the limit of f(x) as x approaches 0 does not exist:
limx→0f(x) does not exist.
- Right-hand limit: limx→0+f(x)=1
Topper's Solved these Questions
- LIMITS AND DERIVATIVESBOOK - MODERN PUBLICATIONCHAPTER - LIMITS AND DERIVATIVESEXERCISE - NCERT FILE - EXERCISE 13.2
27 Videos
- LIMITS AND DERIVATIVESBOOK - MODERN PUBLICATIONCHAPTER - LIMITS AND DERIVATIVESEXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER 13
33 Videos
- LIMITS AND DERIVATIVESBOOK - MODERN PUBLICATIONCHAPTER - LIMITS AND DERIVATIVESEXERCISE - OBJECTIVE TYPE QUESTIONS - (D) VERY SHORT ANSWER TYPE QUESTIONS
25 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - MODERN PUBLICATIONCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - CHAPTER TEST
12 Videos
- LINEAR INEQUATIONSBOOK - MODERN PUBLICATIONCHAPTER - LINEAR INEQUATIONSEXERCISE - CHAPTER TEST
12 Videos
Similar Questions
Find limx→0f(x), where f(x)=|x|−5.
View SolutionFind limx→1f(x), where f(x)={x+1x≠10x=1}
View SolutionEvaluate limx→0f(x), where :
f(x)={x|x|,x≠00,x=0
View SolutionFind limX→0f(x) where f(x)={xx≠05x=0}
View SolutionFind limx→0f(x), where f(x)=⎧⎪⎨⎪⎩x−1x<00x=0x=1x>0
View SolutionFind limx→0f(x) and limx→1f(x), where
f(x)={2x+3,x≤03(x+1),x>0
View SolutionFind (lim)x→0f(x), where f(x)=[x|x|,x≠00,x=0
View SolutionCalculate limx→0f(x), where f(x)=1x2 for x>0
View SolutionEvaluate limx→0f(x), where
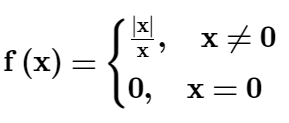
View SolutionEvaluate : limx→0f(x)={|x|x,x≠0 0,x=0.
View Solution
