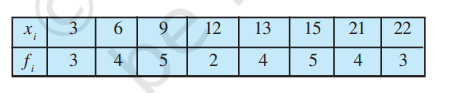
Find the mean deviation from the median for the following data :
38,70,48,34,63,42,55,44,53,47
The correct Answer is:8.6
To find the mean deviation from the median for the given data set, we will follow these steps:
Step 1: Arrange the data in ascending order
The given data is: 38, 70, 48, 34, 63, 42, 55, 44, 53, 47.
Arranging in ascending order:
34, 38, 42, 44, 47, 48, 53, 55, 63, 70.
Step 2: Calculate the median
Since there are 10 observations (an even number), the median is the average of the 5th and 6th terms.
Finding the 5th and 6th terms:
- 5th term = 47
- 6th term = 48
Calculating the median:
Median = (47 + 48) / 2 = 95 / 2 = 47.5.
Step 3: Calculate the absolute deviations from the median
Now we will find the absolute deviations of each observation from the median (47.5).
Calculating absolute deviations:
- |34 - 47.5| = 13.5
- |38 - 47.5| = 9.5
- |42 - 47.5| = 5.5
- |44 - 47.5| = 3.5
- |47 - 47.5| = 0.5
- |48 - 47.5| = 0.5
- |53 - 47.5| = 5.5
- |55 - 47.5| = 7.5
- |63 - 47.5| = 15.5
- |70 - 47.5| = 22.5
Step 4: Sum of absolute deviations
Now, we will sum all the absolute deviations calculated in the previous step.
Summing the absolute deviations:
13.5 + 9.5 + 5.5 + 3.5 + 0.5 + 0.5 + 5.5 + 7.5 + 15.5 + 22.5 = 84.
Step 5: Calculate the mean deviation
The mean deviation is calculated by dividing the sum of absolute deviations by the number of observations.
Calculating mean deviation:
Mean Deviation = Total Absolute Deviations / Number of Observations = 84 / 10 = 8.4.
Final Answer:
The mean deviation from the median for the given data is 8.4.
---
The given data is: 38, 70, 48, 34, 63, 42, 55, 44, 53, 47.
34, 38, 42, 44, 47, 48, 53, 55, 63, 70.
Since there are 10 observations (an even number), the median is the average of the 5th and 6th terms.
- 5th term = 47
- 6th term = 48
Median = (47 + 48) / 2 = 95 / 2 = 47.5.
Now we will find the absolute deviations of each observation from the median (47.5).
- |34 - 47.5| = 13.5
- |38 - 47.5| = 9.5
- |42 - 47.5| = 5.5
- |44 - 47.5| = 3.5
- |47 - 47.5| = 0.5
- |48 - 47.5| = 0.5
- |53 - 47.5| = 5.5
- |55 - 47.5| = 7.5
- |63 - 47.5| = 15.5
- |70 - 47.5| = 22.5
Now, we will sum all the absolute deviations calculated in the previous step.
13.5 + 9.5 + 5.5 + 3.5 + 0.5 + 0.5 + 5.5 + 7.5 + 15.5 + 22.5 = 84.
The mean deviation is calculated by dividing the sum of absolute deviations by the number of observations.
Mean Deviation = Total Absolute Deviations / Number of Observations = 84 / 10 = 8.4.
The mean deviation from the median for the given data is 8.4.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Exercise 15( c) (Short Answer Type Questions)1videos
STATISTICS
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Exercise 15(c ) (Long Answer Type Question - I)8videos
STATISTICS
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Exercise 15(a) (Long Answer Type Questions- II)1videos
STATISTICS
- BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - CHAPTER TEST 112videos
SETS
- BOOK - MODERN PUBLICATIONCHAPTER - STRAIGHT LINES EXERCISE - Chapter test12videos
STRAIGHT LINES
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the mean deviation from the median of the following data
 A7.08B7C7.1D7.05
A7.08B7C7.1D7.05 - Question 2 - Select One
The mean deviation from the mean for the following data is
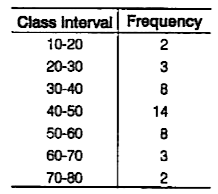 A5B10C15D20
A5B10C15D20 - Question 3 - Select One
The mean deviation from the mean for the following data is
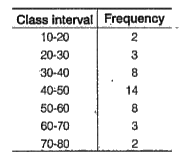 A5B10C15D20
A5B10C15D20
Find the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about the mean for the following data :
 View Solution
View SolutionFind the mean deviation about median for the following data:
 View Solution
View SolutionFind the mean deviation from median for the following tables:
 View Solution
View SolutionFind the mean deviation about median for the following data.
 View Solution
View Solution